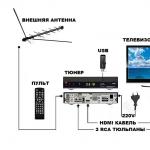
Šiuo metu žinomi šie radijo kanalų organizavimo būdai (radijo technologijos): FDMA, TDMA, CDMA, FH-CDMA. Galimi jų deriniai (pavyzdžiui, FDMA/TDMA). Šių technologijų taikymo laikas iš esmės sutampa su mobiliojo ryšio sistemų kūrimo etapais. Pirmosios kartos mobiliojo radijo telefono įranga naudojo dažnių padalijimo daugkartinės prieigos (FDMA) technologiją. FDMA radijo technologija iki šiol buvo sėkmingai naudojama pažangioje įrangoje korinio ryšio pirmos kartos, taip pat paprastesnėse mobiliojo radijo telefono sistemose, turinčiose ne korinio struktūrą. Kalbant apie pirmojo etapo mobiliojo ryšio standartus, pirmųjų radialinių sistemų standartų sąvoka nebuvo naudojama, o įranga skyrėsi pagal sistemų pavadinimus (Altajaus, Volemot, Actionet ir kt.). Korinio ryšio sistemos pradėjo skirtis pagal standartus. FDMA technologija yra tokių pirmosios kartos korinio ryšio sistemų standartų kaip NMT-450, NMT-900, AMPS, TACS. Antrosios kartos korinio mobiliojo ryšio sistemos perėjo prie skaitmeninio perduodamų balso pranešimų apdorojimo, pradėdamos naudoti laiko padalijimo daugkartinės prieigos (TDMA) radijo technologiją. Dėl perėjimo prie TDMA: padidėjo radijo kelio atsparumas triukšmui, pagerėjo jo apsauga nuo pasiklausymo ir kt. TDMA naudojama sistemose su tokiais standartais kaip GSM, D-AMP(pastarasis amerikietiškoje versijoje dažnai vadinamas tiesiog TDMA). Kodų padalijimo daugialypės prieigos radijo technologija CDMA, arba angliška versija CDMA, viešuosiuose radijo telefonų tinkluose buvo aktyviai įdiegta tik pastaruosius penkerius metus. Ši radijo technologija turi savo privalumų, nes CDMA įrenginiuose: - radijo dažnių spektro naudojimo efektyvumas yra 20 kartų didesnis lyginant su AMPS standarto radijo įranga (FDMA technologija) ir 3 kartus didesnis lyginant su GSM (TDMA technologija); - žymiai geresnė ryšių kokybė, patikimumas ir konfidencialumas nei kitose 2 kartos TDMA sistemose; - galima naudoti mažo dydžio mažos galios gnybtus su ilgas terminas darbas; - tuo pačiu atstumu nuo bazinės stoties CDMA abonentinių terminalų spinduliuotės galia yra daugiau nei 5 kartus mažesnė, palyginti su tuo pačiu rodikliu standartiniuose tinkluose, pagrįstuose kitomis radijo technologijomis; - galima optimizuoti tinklo topologiją skaičiuojant aprėpties sritis. CDMA technologija pirmą kartą buvo įdiegta IS-95 standarto korinio ryšio įrangoje. Pagal savo paslaugų galimybes esamos CDMA sistemos priklauso antros kartos korinio ryšio sistemoms. Remiantis Nacionalinio telekomunikacijų instituto (ETRI) statistika, CDMA tinklo abonentų skaičius kasdien auga 2000 žmonių. Pagal abonentų skaičiaus augimo tempus šie tinklai lenkia kitų esamų korinio ryšio standartų tinklus, aplenkdami net tokio populiaraus standarto kaip GSM korinio ryšio tinklų plėtrą. Šiuo metu CDMA tinkluose yra mažiausiai 30 milijonų abonentų. Pasaulinė telekomunikacijų bendruomenė linkusi manyti, kad CDMA užims lyderio poziciją būsimose abonentinių linijų belaidės prieigos sistemose (trečiosios kartos asmeninių ryšių sistemose). Tokia išvada padaryta dėl to, kad CDMA technologija geriausiai atitinka trečiosios kartos IMT-2000 įrangos reikalavimus, ypač siekiant užtikrinti keitimąsi informacija esant dideliam perdavimo greičiui. Tačiau būsimose bevielės prieigos sistemose numatoma naudoti vadinamąsias plačiajuostes CDMA sistemas, kuriose dažnių juosta vienam kanalui bus ne mažesnė kaip 5 MHz (šiuolaikinėse antrosios kartos CDMA sistemose dažnių juosta vienam kanalui yra 1,23 MHz). Per pastaruosius kelerius metus pradėjo atsirasti įrankių bevielis ryšys, kurios yra pagrįstos dažnio šuolio plitimo spektro (FH-CDMA) technologija. Ši technologija apjungia TDMA specifiką, kai kiekvienas dažnis yra padalintas į keletą laiko tarpsnių, ir CDMA, kai kiekvienas siųstuvas naudoja konkrečią į triukšmą panašių signalų seką. Ši technologija buvo pritaikyta sistemose, skirtose organizuoti fiksuoto ryšio ryšį.

KUR RASTI JŲ CHARAKTERISTIKUS, ŽINAU

44. Periodinių signalų vaizdavimas Furjė eilučių pavidalu

http://scask.ru/book_brts.php?id=8

Periodiniai signalai ir Furjė eilutės

Laikui bėgant pasikartojančio proceso matematinis modelis yra periodinis signalas, turintis tokią savybę:

Čia T yra signalo laikotarpis.

Užduotis – rasti tokio signalo spektrinį skaidymą.

Furjė serija.

Nustatykime laiko intervalą, aptartą skyriuje. I yra ortonormalus pagrindas, sudarytas iš harmoninių funkcijų, turinčių kelis dažnius;

Bet kuri funkcija pagal šį pagrindą atitinka periodiškumo sąlygą (2.1). Todėl šiuo pagrindu atliekant ortogonalinį signalo skaidymą, t.y., apskaičiuojant koeficientus

gauname spektrinį skaidymą

galioja per visą laiko ašies begalybę.

Formos (2.4) serija vadinama tam tikro signalo Furjė serija. Leiskite pristatyti pagrindinį dažnį sekos, kuri sudaro periodinį signalą. Skaičiuodami plėtimosi koeficientus pagal (2.3) formulę, periodiniam signalui rašome Furjė eilutes

su šansais

(2.6)

Taigi, bendruoju atveju periodiniame signale yra nuo laiko nepriklausomas pastovus komponentas ir begalinis harmoninių virpesių rinkinys, vadinamosios harmonikos, kurių dažniai yra sekos pagrindinio dažnio kartotiniai.

Kiekvieną harmoniką galima apibūdinti pagal jos amplitudę ir pradinę fazę, todėl Furjė eilutės koeficientai turi būti parašyti forma

Pakeitę šias išraiškas į (2.5), gauname kitą, lygiavertę Furjė eilutės formą:

kuris kartais pasirodo patogesnis.

Periodinio signalo spektrinė diagrama.

Tai yra tai, kas paprastai vadinama konkretaus signalo Furjė serijos koeficientų grafiniu vaizdu. Yra amplitudės ir fazių spektrinės diagramos (2.1 pav.).

Čia horizontalioji ašis žymi harmoninius dažnius tam tikroje skalėje, o vertikali ašis – jų amplitudes ir pradines fazes.

Ryžiai. 2.1. Kai kurių periodinių signalų spektrinės diagramos: a - amplitudė; b - fazė

Juos ypač domina amplitudės diagrama, kuri leidžia spręsti apie tam tikrų harmonikų procentą periodinio signalo spektre.

Panagrinėkime keletą konkrečių pavyzdžių.

2.1 pavyzdys. Periodinės stačiakampių vaizdo impulsų sekos su žinomais parametrais Furjė serija, net taško t = 0 atžvilgiu.

Radijo inžinerijoje santykis vadinamas sekos darbo ciklu. Naudodami (2.6) formules randame

Formoje patogu parašyti galutinę Furjė serijos formulę

Fig. 2.2 paveiksle parodytos nagrinėjamos sekos amplitudinės diagramos dviem kraštutiniais atvejais.

Svarbu pažymėti, kad trumpų impulsų seka, gana retai sekanti vienas kitą, turi turtingą spektrinę sudėtį.

Ryžiai. 2.2. Stačiakampių vaizdo impulsų periodinės sekos amplitudės spektras: a - su dideliu darbo ciklu; b - su mažu darbo ciklu

2.2 pavyzdys. Furjė serijos periodinės impulsų sekos, sudarytos iš harmoninio signalo, kurio forma ribojama lygiu (manoma, kad ).

Įveskime specialų parametrą – ribinį kampą, nustatytą pagal santykį kur

Pagal tai vertė yra lygi vieno impulso trukmei, išreikštai kampu:

Impulso, generuojančio nagrinėjamą seką, analitinis įrašymas turi formą

Pastovios sekos komponentas

Pirmasis harmoninės amplitudės koeficientas

Panašiai apskaičiuojamos harmoninių komponentų amplitudės

Gauti rezultatai paprastai rašomi taip:

kur veikia vadinamosios Bergo funkcijos:

Kai kurių Bergo funkcijų grafikai parodyti Fig. 2.3.

Ryžiai. 2.3. Pirmųjų kelių Bergo funkcijų grafikai

Signalų spektrinis tankis. Tiesioginės ir atvirkštinės Furjė transformacijos.

Signalas vadinamas periodiškai, jei jo forma laike pasikartoja cikliškai. Periodinis signalas bendra forma rašomas taip:

Čia yra signalo laikotarpis. Periodiniai signalai gali būti paprasti arba sudėtingi.

Periodinių signalų matematiniam vaizdui su tašku dažnai naudojama ši serija, kurioje kaip bazinės funkcijos pasirenkami kelių dažnių harmoniniai (sinuso ir kosinuso) virpesiai:

Kur. - funkcijų sekos pagrindinis kampinis dažnis. Harmoninių pagrindų funkcijoms iš šios serijos gauname Furjė eilutę, kurią paprasčiausiu atveju galima parašyti tokia forma:

kur yra koeficientai

Iš Furjė serijos aišku, kad bendruoju atveju periodinis signalas turi pastovų komponentą ir pagrindinio dažnio harmoninių virpesių rinkinį ir jo harmoniką su dažniais. Kiekvienam Furjė serijos harmoniniam virpesiui būdinga amplitudė ir pradinė fazė.

Spektrinė diagrama ir periodinio signalo spektras.

Jei kuris nors signalas pateikiamas kaip skirtingų dažnių harmoninių virpesių suma, tai reiškia, kad spektrinis skilimas signalas.

Spektrinė diagrama signalas yra grafinis šio signalo Furjė serijos koeficientų vaizdas. Yra amplitudės ir fazių diagramos. Norint sudaryti šias diagramas, harmoninių dažnių reikšmės brėžiamos tam tikra skale išilgai horizontalios ašies, o jų amplitudės ir fazės – išilgai vertikalios ašies. Be to, harmonikų amplitudės gali turėti tik teigiamas reikšmes, fazės intervale gali turėti ir teigiamas, ir neigiamas reikšmes.

Periodinio signalo spektrinės diagramos:

a) - amplitudė; b) - fazė.

Signalo spektras- tai harmoninių komponentų rinkinys su konkrečiomis dažnių, amplitudių ir pradinių fazių reikšmėmis, kurios kartu sudaro signalą. Praktiškai spektrinės diagramos vadinamos trumpiau - amplitudės spektras, fazių spektras. Didžiausią susidomėjimą rodo amplitudės spektrinė diagrama. Jis gali būti naudojamas norint įvertinti harmonikų procentą spektre.

Spektrinės charakteristikos vaidina didelį vaidmenį telekomunikacijų technologijose. Žinodami signalo spektrą, galite teisingai apskaičiuoti ir nustatyti stiprintuvų, filtrų, kabelių ir kitų ryšio kanalų mazgų pralaidumą. Signalų spektrų žinios būtinos kuriant daugiakanales sistemas su dažnių padalijimu. Nežinant trukdžių spektro sunku imtis priemonių jam slopinti.

Iš to galime daryti išvadą, kad spektras turi būti žinomas, kad būtų galima atlikti neiškraipytą signalo perdavimą ryšio kanalu, užtikrinti signalo atskyrimą ir sumažinti trukdžius.

Signalų spektrams stebėti yra prietaisai, vadinami spektro analizatoriai. Jie leidžia stebėti ir matuoti atskirų periodinio signalo spektro komponentų parametrus, taip pat matuoti spektrinis tankis nuolatinis signalas.

Dažnai matematiškai aprašyti net ir paprastos struktūros ir formos deterministinius signalus yra sudėtinga užduotis. Todėl naudojama originali technika, kai realūs kompleksiniai signalai pakeičiami (atvaizduojami, aproksimuojami) elementariomis funkcijomis aprašomų matematinių modelių rinkiniu (svertine suma, t.y. serija). Tai yra svarbus įrankis analizuojant elektrinių signalų perdavimą per elektronines grandines. Be to, signalo atvaizdavimas taip pat gali būti naudojamas kaip jo aprašymo ir analizės šaltinis. Tokiu atveju galite žymiai supaprastinti atvirkštinę problemą - sintezė sudėtingi signalai iš elementariųjų funkcijų rinkinio.

Periodinių signalų spektrinis vaizdavimas Furjė serijomis

Apibendrinta Furjė serija.

Pagrindinė signalų (funkcijų) spektrinio vaizdavimo idėja kilo daugiau nei prieš 200 metų ir priklauso fizikui ir matematikui J. B. Fourier.

Panagrinėkime elementariųjų stačiakampių funkcijų sistemas, kurių kiekviena gaunama iš vienos pradinės - prototipo funkcijos. Ši prototipo funkcija veikia kaip „statybinis blokas“, o norima aproksimacija randama tinkamai derinant identiškus blokus. Furjė parodė, kad bet kuri sudėtinga funkcija gali būti pavaizduota (apytiksliai) kaip baigtinė arba begalinė kelių harmoninių virpesių su tam tikromis amplitudėmis, dažniais ir pradinėmis fazėmis serijos suma. Ši funkcija visų pirma gali būti srovė arba įtampa grandinėje. Saulės spindulys, prizmės išskaidytas į spalvų spektrą, yra fizikinis matematinių Furjė transformacijų analogas (2.7 pav.).

Iš prizmės sklindanti šviesa erdvėje suskirstoma į atskiras grynas spalvas arba dažnius. Spektras turi vidutinę kiekvieno dažnio amplitudę. Taigi, intensyvumo ir laiko funkcija buvo transformuota į amplitudės ir dažnio funkciją. Paprasta Furjė samprotavimų iliustracija parodyta Fig. 2.8. Periodinė, gana sudėtingos formos kreivė (2.8 pav., A) - tai dviejų skirtingų, bet kelių dažnių harmonikų suma: viena (2.8 pav., b) ir padvigubėjo (2.8 pav., V).

Ryžiai. 2.7.

Ryžiai. 2.8.

A- kompleksinis svyravimas; b,c- 1-asis ir 2-asis apytikslis signalas

Naudojant Furjė spektrinę analizę, sudėtinga funkcija vaizduojama kaip harmonikų suma, kurių kiekviena turi savo dažnį, amplitudę ir pradinę fazę. Furjė transformacija apibrėžia funkcijas, vaizduojančias tam tikrą dažnį atitinkančių harmoninių komponentų amplitudę ir fazę, o fazė yra sinusinės bangos pradžios taškas.

Transformaciją galima gauti dviem skirtingais matematiniais metodais, iš kurių vienas naudojamas, kai originali funkcija tęstinis, o kitas, kai jį suteikia daug atskirų atskirų reikšmių.

Jei tiriama funkcija gaunama iš reikšmių su tam tikrais diskretiškais intervalais, tada ją galima suskirstyti į nuoseklias sinusoidinių funkcijų serijas su diskretišku dažniu – nuo ​​žemiausio, pagrindinio ar pagrindinio dažnio, o paskui su dažniais, padvigubinamais, trigubais. ir kt. virš pagrindinės. Ši komponentų suma vadinama šalia Furjė.

Ortogonaliniai signalai. Patogiu būdu Spektrinis signalo aprašymas pagal Furjė yra jo analitinis atvaizdavimas naudojant stačiakampių elementariųjų laiko funkcijų sistemą. Tebūnie Hilberto signalų erdvė u0(t)m G/,(?), ..., u n (t) su ribota energija, apibrėžta per baigtinį arba begalinį laiko intervalą (t v 1 2). Šiame segmente apibrėžsime begalinę tarpusavyje susijusių elementariųjų laiko funkcijų sistemą (poaibį) ir pavadinsime ją pagrindinis“.

Kur g = 1, 2, 3,....

Funkcijos u(t) Ir v(t) yra stačiakampiai intervale (?, ? 2), jei jų skaliarinė sandauga, su sąlyga, kad nė viena iš šių funkcijų nėra identiška nuliui.

Matematikoje tai apibrėžiama Hilberto signalų erdvėje stačiakampių koordinačių pagrindas, t.y. stačiakampių bazinių funkcijų sistema.

Funkcijų (signalų) ortogonalumo savybė siejama su jų apibrėžimo intervalu (2.9 pav.). Pavyzdžiui, du harmoniniai signalai m,(?) = = sin(2nr/7’ 0) ir u., (t)= nuodėmė(4 nt/T Q)(t. y. su dažniais / 0 = 1/7’ 0 ir 2/0) yra stačiakampiai per bet kurį laiko intervalą, kurio trukmė lygi sveikajam pusciklų skaičiui T 0(2.9 pav., A). Todėl pirmuoju laikotarpiu signalai ir (1) Ir u2(t) yra stačiakampiai intervale (0,7" 0 /2); bet intervale (O, ZG 0 /4) jie yra nestačiakampiai. Pa 2.9 pav., b signalai yra stačiakampiai dėl skirtingo jų atsiradimo laiko.

Ryžiai. 2.9.

A- ant intervalo; b - dėl skirtingo pasirodymo laiko Signalo pateikimas u(t) elementarieji modeliai gerokai supaprastinami, jei pasirenkama bazinių funkcijų sistema vff), turėdamas nuosavybę ortonormalumas. Iš matematikos žinoma, ar kuri nors stačiakampės sistemos (2.7) funkcijų pora tenkina sąlygą

tada funkcijų sistema (2.7) ortonormalus.

Matematikoje tokia (2.7) formos bazinių funkcijų sistema vadinama ortonormalus pagrindas.

Tegu tam tikru laiko intervalu |r, t 2| aktyvus savavališkas signalas u(t) o jai pavaizduoti naudojama ortonormali funkcijų sistema (2.7). Savavališkas signalų projektavimas u(t) koordinačių ašyje vadinamas pagrindas išplėtimas į apibendrintą Furjė eilutę.Šis išplėtimas turi formą

kur c yra kai kurie pastovūs koeficientai.

Koeficientams nustatyti iš į apibendrinta Furjė eilutė, pasirenkame vieną iš pagrindinių funkcijų (2.7) v k (t) s bet koks skaičius Į. Padauginkime abi išplėtimo puses (2.9) iš šios funkcijos ir sujungsime rezultatą laikui bėgant:

Dėl pasirinktų funkcijų pagrindo ortonormalumo šios lygybės dešinėje pusėje visos sumos sąlygos i ^ Į nueis į nulį. Tik vienintelis sumos narys, turintis skaičių, liks ne nulis i = į,Štai kodėl

Formos gaminys c k v k (t),įtraukta į apibendrintą Furjė eilutę (2.9), yra spektrinis komponentas signalas u(t), ir koeficientų rinkinys (signalų vektorių projekcijos koordinačių ašyse) (с 0 , с,..., iš į,..., s„) visiškai nustato analizuojamą signalą ii(t) ir vadinasi spektras(iš lat. spektras- vaizdas).

Esmė spektrinis vaizdavimas (analizė) signalą sudaro koeficientų nustatymas su i pagal (2.19) formulę.

Racionalios ortogonalios funkcijų koordinačių pagrindo sistemos pasirinkimas priklauso nuo tyrimo tikslo ir yra nulemtas siekio maksimaliai supaprastinti matematinį analizės, transformavimo ir duomenų apdorojimo aparatą. Bazinėmis funkcijomis šiuo metu naudojami Chebyshev, Hermite, Laguerre, Legendre ir kt.. Labiausiai paplitusi signalų transformacija harmoninių funkcijų bazėse: kompleksinė eksponentinė exp (J 2 pėdos) ir tikrosios trigonometrinės sinuso-kosinuso funkcijos, susietos Eulerio formule e>x= cosx + y"sinx. Tai paaiškinama tuo, kad harmoninis virpesys teoriškai visiškai išlaiko savo formą, eidamas per tiesines grandines su pastoviais parametrais, ir keičiasi tik jo amplitudė ir pradinė fazė. Simbolinis metodas, gerai išvystytas grandinės teorijoje taip pat plačiai naudojamas.. Deterministinių signalų vaizdavimo pastovių komponentų rinkinio forma operacija ( pastovus komponentas) o harmoninių virpesių su daugybe dažnių suma paprastai vadinama spektrinis skilimas. Gana plačiai paplitęs apibendrintos Furjė serijos naudojimas signalų teorijoje taip pat siejamas su labai svarbia jos savybe: su pasirinkta ortonormalia funkcijų sistema. vk(t) ir fiksuotas serijos terminų skaičius (2.9), jis geriausiai atvaizduoja tam tikrą signalą u(t).Ši Furjė serijos savybė yra plačiai žinoma.

Spektriniame signalų atvaizdavime plačiausiai naudojamos ortonormalios bazės. trigonometrinės funkcijos. Taip yra dėl šių priežasčių: harmoninius virpesius generuoti lengviausia; harmoniniai signalai yra nekintami transformacijų, atliekamų stacionariomis tiesinėmis elektros grandinėmis, atžvilgiu.

Įvertinkime laiko ir spektro reprezentacijas analoginis signalas(2.10 pav.). Fig. 2.10, A parodyta sudėtingo nuolatinio signalo laiko diagrama, o Fig. 2.10, b - jo spektrinis skilimas.

Periodinių signalų spektrinį atvaizdavimą nagrinėkime kaip harmoninių funkcijų arba kompleksinių eksponentų, kurių dažniai sudaro aritmetinę progresiją, sumą.

Periodinis jie vadina signalą u„(?). kartojant reguliariais intervalais (2.11 pav.):

kur Г yra impulsų pasikartojimo arba pasikartojimo laikotarpis; n = 0,1, 2,....

Ryžiai. 2.11. Periodinis signalas

Jeigu T yra signalo laikotarpis u(t), tada periodai taip pat bus jo kartotiniai: 2G, 3 T ir tt Periodinė impulsų seka (jie vadinami vaizdo impulsai) apibūdinama išraiška

Ryžiai. 2.10.

A- laiko diagrama; b- amplitudės spektras

Čia uQ(t)- vieno impulso forma, kuriai būdinga amplitudė (aukštis) h = E, trukmė t„, stebėjimo laikotarpis T = 1/F(F – dažnis), pvz., impulsų padėtis laike, palyginti su laikrodžio taškais t = 0.

Periodinių signalų spektrinei analizei patogi stačiakampė sistema (2.7) harmoninių funkcijų pavidalu su keliais dažniais:

kur co, = 2p/T- pulso pasikartojimo dažnis.

Skaičiuojant integralus pagal formulę (2.8), nesunku patikrinti šių funkcijų ortogonalumą intervale [-Г/2, Г/2|. Bet kuri funkcija atitinka periodiškumo sąlygą (2.11), nes jų dažniai yra kartotiniai. Jei sistema (2.12) parašyta kaip

tada gauname ortonormalų harmoninių funkcijų pagrindą.

Įsivaizduokime periodinį signalą, labiausiai paplitusią signalų teorijoje trigonometrinis(sinuso kosinusas) figūra Furjė serija:

Iš matematikos kurso žinoma, kad ekspansija (2.11) egzistuoja, t.y. serija suartėja, jei funkcija (šiuo atveju signalas) u(t) intervale [-7/2, 7/2] tenkina Dirichlet sąlygos(skirtingai nei Dirichlet teorema, jie dažnai interpretuojami supaprastintai):

• neturėtų būti 2-osios rūšies nutrūkimų (su šakomis einančiomis į begalybę);
• funkcija yra apribota ir turi baigtinį skaičių 1-osios rūšies nutrūkimų (šuoliukų);
• funkcija turi baigtinį ekstremalių skaičių (t. y. maksimumus ir minimumus).

Formulėje (2.13) yra šie analizuojamo signalo komponentai:

Nuolatinis komponentas

Kosinuso komponentų amplitudės

Sinusoidinių komponentų amplitudės

Ryšio teorijoje vadinamas spektrinis komponentas su dažniu co Pirmas (pagrindinis) harmoninė, ir komponentai su dažniais ISO, (n> 1) - aukštesnės harmonikos periodinis signalas. Dažnio pakopa Aco tarp dviejų gretimų sinusoidų iš Furjė plėtimosi vadinama dažnio skiriamoji geba spektras

Jei signalas yra lyginė laiko funkcija u(t) = u(-t), tada Furjė eilutės trigonometriniame vaizde (2.13) sinusoidinių koeficientų nėra b n, nes pagal (2.16) formulę jie išnyksta. Dėl signalo u(t), apibūdinamas nelygine laiko funkcija, priešingai, pagal (2.15) formulę kosinuso koeficientai lygūs nuliui a p(nuolatinis komponentas a 0 taip pat nėra), o serijoje yra komponentų b p.

Integravimo ribos (nuo -7/2 iki 7/2) neturi būti tokios pat kaip formulėse (2.14)-(2.16). Integruoti galima bet kuriuo 7 pločio laiko intervalu – rezultatas nepasikeis. Konkrečios ribos pasirenkamos dėl skaičiavimo patogumo; pavyzdžiui, gali būti lengviau integruoti nuo O iki 7 arba nuo -7 iki 0 ir pan.

Matematikos šaka, nustatanti ryšį tarp laiko funkcijos u (t) ir spektrinius koeficientus a p, b p, paskambino harmoninė analizė dėl funkcijos ryšio u(t) su šios sumos sinusu ir kosinusu. Be to, spektrinė analizė daugiausia apsiriboja harmoninės analizės sistema, kuri randa išskirtinį pritaikymą.

Dažnai Furjė serijos sinuso ir kosinuso formos naudojimas nėra visiškai patogus, nes kiekvienai sumavimo indekso vertei P(t.y. kiekvienai harmonikai, kurios dažnis mOj) formulėje (2.13) atsiranda du terminai - kosinusas ir sinusas. Matematiniu požiūriu patogiau šią formulę pavaizduoti lygiaverte Furjė eilute tikroji forma/.

Kur A 0 = a 0 / 2; A n = yja 2 n + b - amplitudė; n-osios harmonikos signalas. Kartais santykyje (2.17) prieš cp L dedamas „pliuso“ ženklas, tada pradinė harmonikų fazė rašoma kaip cp u = -arctg ( b n fa n).

Signalų teorijoje plačiai naudojama kompleksinė Furjė serijos forma. Jis gaunamas iš tikrosios eilutės formos, pavaizduojant kosinusą kaip pusę kompleksinių eksponentų sumos, naudojant Eilerio formulę:

Kreipdamiesi ši transformacijaĮ realiąją Furjė eilutės formą (2.17), gauname kompleksinių eksponentų su teigiamais ir neigiamais eksponentais sumas:

O dabar (2.19) formulėje rodytuvus, kurių dažnis с, su minuso ženklu rodiklyje, interpretuosime kaip serijos su neigiamais skaičiais narius. Taikant tą patį metodą, koeficientas A 0 taps serialo, kurio numeris nulis, nare. Po paprastų transformacijų pasiekiame sudėtinga forma Furjė serija

Kompleksinė amplitudė P th harmonikos.

Vertybės S p teigiamais ir neigiamais skaičiais P yra sudėtingi konjugatai.

Atkreipkite dėmesį, kad Furjė serija (2.20) yra sudėtingų eksponentų visuma exp(jn(o (t) su dažniais, formuojančiais aritmetinę progresiją.

Nustatykime ryšį tarp Furjė eilutės trigonometrinių ir kompleksinių formų koeficientų. Tai akivaizdu

Taip pat galima parodyti, kad koeficientai a p= 2C w coscp„; b n = 2C/I sincp, f .

Jeigu u(t) yra lyginė funkcija, C serijos koeficientai bus tikras, ir jeigu u(t) – funkcija yra nelyginė, serijos koeficientai taps įsivaizduojamas.

Periodinio signalo spektrinis vaizdavimas Furjė serijos kompleksine forma (2.20) turi ir teigiamų, ir neigiamų dažnių. Tačiau neigiamų dažnių gamtoje nėra, ir tai yra matematinė abstrakcija (fizinė neigiamo dažnio reikšmė yra sukimasis priešinga kryptimi, nei laikoma teigiama). Jie atsiranda kaip formalaus harmoninių virpesių atvaizdavimo sudėtingoje formoje pasekmė. Pereinant nuo kompleksinės žymėjimo formos (2.20) prie tikrosios formos (2.17), neigiamas dažnis išnyksta.

Signalo spektras vizualiai vertinamas pagal jo grafinį vaizdą – spektrinę diagramą (2.12 pav.). Išskirti amplitudė-dažnis Ir fazinio dažnio spektrai. Harmoninių amplitudių rinkinys A p(2.12 pav., A) paskambino amplitudės spektras, jų fazės (2.12 pav., b) Trečiadienis aš - fazių spektras. Visumą S p = |S p yra kompleksinis amplitudės spektras(2.12 pav., V). Spektrinėse diagramose abscisių ašys rodo srovės dažnį, o ordinačių ašys rodo atitinkamų analizuojamo signalo harmoninių komponentų tikrąją arba kompleksinę amplitudę arba fazę.

Ryžiai. 2.12.

A - amplitudė; b - fazė; V - kompleksinės Furjė serijos amplitudės spektras

Periodinio signalo spektras vadinamas valdė arba diskretus, nes jis susideda iš atskirų linijų, kurių aukštis lygus amplitudei A p harmonikų Iš visų spektrų tipų amplitudės spektrai yra informatyviausi, nes jie leidžia įvertinti kiekybinį tam tikrų harmonikų kiekį signalo dažninėje kompozicijoje. Signalų teorijoje įrodyta, kad amplitudės spektras yra tolygaus dažnio funkcija, ir fazė - nelyginis.

Pastaba lygiu atstumu(lygus atstumas nuo koordinačių pradžios) periodinių signalų kompleksinio spektro: simetriški (teigiami ir neigiami) dažniai, kuriuose yra trigonometrinės Furjė serijos spektriniai koeficientai, sudaro vienodo atstumo seką (..., -Zho v..., -2so p -so p 0, v 2 taigi,..., ncov...), kurio dažnis co = 0 ir žingsnis co t = 2l/7’. Koeficientai gali turėti bet kokią reikšmę.

2.1 pavyzdys

Apskaičiuokime periodinės stačiakampių impulsų sekos su amplitudė?, trukme m ir pasikartojimo periodu amplitudę ir fazių spektrus T. Signalas yra lygi funkcija (2.13 pav.).

Ryžiai. 2.13.

Sprendimas

Yra žinoma, kad idealus stačiakampis vaizdo impulsas apibūdinamas tokia lygtimi:

tie. jis susidaro kaip dviejų vienetinių funkcijų skirtumas a(?) (įtraukimo funkcijos), perkeltos laike tn.

Stačiakampių impulsų seka yra žinoma pavienių impulsų suma:

Kadangi duotas signalas yra lyginė laiko funkcija ir per vieną periodą veikia tik intervalą [t ir /2, t ir /2], tai pagal (2.14) formulę

Kur q = T/ T".

Analizuodami gautą formulę, matote, kad pasikartojimo laikotarpis ir impulso trukmė yra įtraukti į ją santykio pavidalu. Ši parinktis q- vadinamas periodo ir impulsų trukmės santykis darbo ciklas periodinė impulsų seka (užsienio literatūroje vietoj darbo ciklo naudojama atvirkštinė vertė - darbo ciklas, iš anglų kalbos, darbo ciklas, lygus m ir /7); adresu q = 2 vadinama stačiakampių impulsų seka, kai impulsų trukmės ir intervalai tarp jų tampa vienodi. vingiuoti(iš graikų kalbos paiav5poq – raštas, geometrinis ornamentas).

Dėl funkcijos, apibūdinančios analizuojamą signalą, pariteto Furjė eilutėje kartu su pastoviuoju komponentu bus tik kosinuso komponentai (2.15):

Dešinėje (2.22) formulės pusėje antrasis veiksnys turi elementariosios funkcijos (sinx)/x formą. Matematikoje ši funkcija žymima sinc(x) ir tik reikšmei X= 0 tai lygu vienetui (lim (sinx/x) =1), praeina

per nulį taškuose x = ±l, ±2l,... ir nyksta didėjant argumentui x (2.14 pav.). Galiausiai trigonometrinė Furjė eilutė (2.13), kuri aproksimuoja duotą signalą, įrašoma forma

Ryžiai. 2.14. Funkcijos grafikas sinx/x

Sinuso funkcija turi žiedlapių pobūdį. Kalbant apie skilčių plotį, reikia pabrėžti, kad periodinių signalų diskrečiųjų spektrų grafikuose galimi du horizontalios ašies kalibravimo variantai - harmoniniais skaičiais ir dažniais. Pavyzdžiui, pav. 2.14 Ordinačių ašis sukalibruota taip, kad atitiktų dažnius. Skilčių plotis, matuojamas harmonikų skaičiumi, yra lygus sekos darbo ciklui. Tai reiškia svarbią stačiakampių impulsų sekos spektro savybę - joje nėra (turi nulinės amplitudės) harmonikų su skaičiais, kurie yra darbo ciklo kartotiniai. Kai impulsų darbo ciklas yra trys, kas trečia harmonika išnyksta. Jei darbo ciklas būtų lygus dviem, tai spektre liktų tik nelyginės pagrindinio dažnio harmonikos.

Iš (2.22) formulės ir pav. 2.14 iš to seka, kad kai kurių aukštesnių signalo harmonikų koeficientai turi neigiamą ženklą. Taip yra dėl to, kad pradinė šių harmonikų fazė yra lygi P. Todėl formulė (2.22) paprastai pateikiama modifikuota forma:

Įrašant Furjė seriją, visų aukštesnių harmonikų komponentų amplitudės vertės spektrinės diagramos grafike yra teigiamos (2.15 pav., A).

Signalo amplitudės spektras labai priklauso nuo pasikartojimo periodo santykio T ir impulso trukmė t ir, t.y. nuo darbo ciklo q. Dažnio atstumas tarp gretimų harmonikų yra lygus impulsų pasikartojimo dažniui, kai 1 = 2l/T. Spektro skilčių plotis, matuojamas dažnio vienetais, lygus 2π/tn, t.y. yra atvirkščiai proporcinga impulso trukmei. Atkreipkite dėmesį, kad esant tokiai pačiai impulso trukmei m ir didėjant ne

Ryžiai. 2.15.

A- amplitudė;b- fazė

jų pasikartojimo laikotarpis T pagrindinis dažnis co mažėja ir spektras tampa tankesnis.

Tas pats vaizdas stebimas, jei impulso trukmė t sutrumpinama, o periodas išlieka nepakitęs T. Visų harmonikų amplitudės mažėja. Tai bendrojo dėsnio apraiška (W. Heisenbergo neapibrėžtumo principas – Neapibrėžtumo principas)“, Kuo trumpesnė signalo trukmė, tuo platesnis jo spektras.

Komponentų fazės nustatomos pagal formulę cp = arctg (mlrd. per metus). Kadangi čia koeficientai b„= 0, tada

Kur m = 0, 1, 2,....

Ryšys (2.24) rodo, kad skaičiuojant spektrinių komponentų fazes susiduriame su matematine neapibrėžtimi. Norėdami jį atskleisti, atsigręžkime į formulę (2.22), pagal kurią harmonikų amplitudės periodiškai keičia ženklą pagal funkcijos sin(nco 1 x 1I /2) ženklo kitimą. Ženklo keitimas formulėje (2.22) yra tolygus šios funkcijos fazės perkėlimui P. Todėl kai šią funkciją teigiama harmoninė fazė (p u = 2 tp, o kai neigiamas – = (2t + 1 )Į(2.15 pav., b). Atkreipkite dėmesį, kad nors stačiakampių impulsų spektro komponentų amplitudės mažėja didėjant dažniui (žr. 2.15 pav. A),šis nykimas yra gana lėtas (amplitudės mažėja atvirkščiai proporcingai dažniui). Norint tokius impulsus perduoti be iškraipymų, reikalinga begalinė ryšio kanalo dažnių juosta. Esant santykinai subtiliems iškraipymams, dažnių juostos ribinė vertė turėtų būti daug kartų didesnė už impulso trukmės atvirkštinę vertę. Tačiau visi tikrieji kanalai turi ribotą dažnių juostos plotį, o tai lemia perduodamų impulsų formos iškraipymus.

Furjė savavališkų periodinių signalų serijoje gali būti be galo daug terminų. Skaičiuojant tokių signalų spektrus, begalinės Furjė eilutės sumos apskaičiavimas sukelia tam tikrų sunkumų ir ne visada reikalingas, todėl apsiribojame baigtinio terminų skaičiaus sumavimu (eilutė „sutrumpa“).

Signalo aproksimacijos tikslumas priklauso nuo sumuojamų komponentų skaičiaus. Panagrinėkime tai naudodami aproksimacijos pagal stačiakampių impulsų sekos pirmųjų aštuonių harmonikų sumą pavyzdį (2.16 pav.). Signalas turi vienpolio vingio formą su pasikartojimo periodu Tai amplitudė E= 1 ir impulso trukmė t ir = T/2 (nurodytas signalas – lygi funkcija – 2.16 pav., A; darbo ciklas q= 2). Aproksimacija parodyta fig. 2.16, b, o grafikai rodo sumuojamų harmonikų skaičių. Vykdant tam tikro periodinio signalo aproksimaciją (žr. 2.13 pav.) trigonometrine seka (2.13), pirmosios ir aukštesnės harmonikos sumavimas bus atliekamas tik per nelyginius koeficientus. Pu nes jei jų reikšmės ir impulso trukmė yra lygūs, m ir = T/2 = = tm/co, reikšmė sin(mo,T H /2) = sin(wt/2) tampa lygi nuliu.

Furjė eilutės (2.23) trigonometrinė forma tam tikram signalui turi formą

Ryžiai. 2.16.

A - duotas signalas; 6 - tarpiniai sumavimo etapai

Kad būtų lengviau pateikti, Furjė eilutę (2.25) galima parašyti supaprastintą:

Iš (2.26) formulės akivaizdu, kad harmonikos, kurios apytiksliai atitinka meandrą, yra nelyginės, turi kintamus ženklus, o jų amplitudės atvirkščiai proporcingos skaičiams. Atkreipkite dėmesį, kad stačiakampių impulsų seka yra prastai tinkama Furjė serijai pavaizduoti – aproksimacija apima bangavimą ir šuoliais, o bet kokio skaičiaus harmoninių komponentų su bet kokia amplitude suma visada bus nuolatinė funkcija. Todėl Furjė serijos elgesys šalia nenutrūkstamų yra ypač įdomus. Iš grafikų pav. 2.16, b nesunku pastebėti, kaip, padidėjus sumuojamų harmonikų skaičiui, gauta funkcija vis labiau artėja prie pradinio signalo formos u(t) visur, išskyrus jos lūžio taškus. Netoli nenutrūkstamumo taškų Furjė eilutės sumavimas suteikia nuolydį, o gautos funkcijos nuolydis didėja sumuojamų harmonikų skaičiumi. Pačiame nutrūkimo taške (pavadinkime jį kaip t = t 0) Furjė serija u(t 0) susilieja į pusę dešiniųjų ir kairiųjų ribų sumos:

Aproksimuotos kreivės atkarpose, esančiose greta pertrūkio, serijų suma duoda pastebimus pulsavimus, o fig. 2.16 aišku, kad šių pulsacijų pagrindinio viršįtampio amplitudė nemažėja didėjant sumuojamų harmonikų skaičiui – ji tik suspaudžiama horizontaliai, artėjant prie lūžio taško.

At P-? lūžio taškuose išstūmimo amplitudė išlieka pastovi,

o jo plotis bus be galo siauras. Tiek santykinė pulsacijų amplitudė (šuolių amplitudės atžvilgiu), tiek santykinis slopinimas nesikeičia; Keičiasi tik pulsavimo dažnis, kurį lemia paskutinių sumuojamų harmonikų dažnis. Taip yra dėl Furjė eilutės konvergencijos. Paimkime klasikinį pavyzdį: ar kada nors pasieksite sieną, jei kiekvienu žingsniu nueisite pusę likusio atstumo? Pirmas žingsnis nuves į pusiaukelę, antrasis – iki trijų ketvirčių, o po penkto žingsnio būsite įveikę beveik 97% kelio. Jūs beveik ten, bet kad ir kiek žingsnių į priekį žengtumėte, griežtąja matematine prasme to niekada nepasieksite. Jūs galite tik matematiškai įrodyti, kad galų gale galėsite priartėti prie bet kokio atstumo, nesvarbu, koks mažas. Šis įrodymas prilygtų parodymui, kad skaičių suma yra 1/2, 1/4, 1/8, 1/16 ir kt. linkęs į vienybę. Šis reiškinys, būdingas visoms Furjė serijoms, skirtoms signalams su 1-ojo tipo netolydumu (pavyzdžiui, šuoliais, kaip ir stačiakampių impulsų frontuose), vadinamas Gibbso efektas*. Tokiu atveju pirmojo (didžiausio) amplitudės bangos vertė aproksimuotoje kreivėje yra apie 9% šuolio lygio (žr. 2.16 pav. P = 4).

Gibbso efektas sukelia nepašalinamą periodinių impulsų signalų aproksimavimo klaidą su 1 tipo nepertraukiamumu. Poveikis atsiranda, kai smarkiai pažeidžiamas funkcijų monotoniškumas. Žirgų lenktynėse poveikis yra didžiausias, visais kitais atvejais pulsacijų amplitudė priklauso nuo monotonijos pažeidimo pobūdžio. Daugeliui praktinių pritaikymų Gibbso efektas sukelia tam tikrų problemų. Pavyzdžiui, garso atkūrimo sistemose šis reiškinys vadinamas „skambėjimu“ arba „mirksėjimu“. Be to, kiekvieną aštrų priebalsį ar kitą staigų garsą gali lydėti trumpas, nemalonus ausiai garsas.

Furjė serija gali būti taikoma ne tik periodiniams, bet ir ribotos trukmės signalams. Šiuo atveju laikas nurodomas

nalinis intervalas, kuriam sudaroma Furjė serija, o kitu metu signalas laikomas lygiu nuliui. Norint apskaičiuoti serijos koeficientus, šis metodas reiškia periodinis tęsinys signalas už nagrinėjamo intervalo ribų.

Atkreipkite dėmesį, kad gamta (pavyzdžiui, žmogaus klausa) naudoja harmoninių signalų analizės principą. Asmuo atlieka virtualų Furjė transformaciją, kai tik išgirsta garsą: ausis tai atlieka automatiškai, pateikdama garsą kaip nuoseklių skirtingų tonų garsumo verčių spektrą. Žmogaus smegenys šią informaciją paverčia suvokiamu garsu.

Harmoninė sintezė. Signalų teorijoje jie plačiai naudojami kartu su harmonine signalų analize harmoninė sintezė- nustatyti sudėtingos formos virpesius sumuojant jų spektro harmoninių komponentų skaičių. Iš esmės aukščiau buvo atlikta periodinės stačiakampių impulsų sekos sintezė iš daugelio harmonikų suma. Praktiškai šios operacijos atliekamos kompiuteriu, kaip parodyta pav. 2.16, b.

• Žanas Baptistas Džozefas Furjė (J.B.J. Fourier; 1768-1830) – prancūzų matematikas ir fizikas.
• Josiah Gibbs (J. Gibbs, 1839-1903) – amerikiečių fizikas ir matematikas, vienas iš cheminės termodinamikos ir statistinės fizikos pradininkų.

Furjė serijos įrašymo formos. Signalas vadinamas periodiškai, jei jo forma laike kartojasi cikliškai Periodinis signalas u(t) apskritai parašyta taip:

u(t)=u(t+mT), m=0, ±1, ±2,…

Čia yra signalo T periodas. Periodiniai signalai gali būti paprasti arba sudėtingi.

Periodinių signalų su tašku matematiniam atvaizdavimui T dažnai naudojama serija (2.2), kurioje bazinėmis funkcijomis pasirenkami kelių dažnių harmoniniai (sinuso ir kosinuso) virpesiai

y 0 (t) = 1; y 1 (t) = sinw 1 t; y 2 (t) = cosw 1 t;

y 3 (t) = sin2w 1 t; y 4 (t) = cos2w 1 t; ..., (2.3)

kur w 1 =2p/T yra pagrindinis sekos kampinis dažnis

funkcijas. Harmoninių pagrindų funkcijoms iš serijos (2.2) gauname Furjė eilutes (Žanas Furjė – XIX a. prancūzų matematikas ir fizikas).

Furjė eilutės formos (2.3) harmoninės funkcijos turi šiuos privalumus: 1) paprastas matematinis aprašymas; 2) tiesinių transformacijų invariancija, t.y. jei tiesinės grandinės įėjime yra harmoninis svyravimas, tai jos išėjime taip pat bus harmoninis virpesys, besiskiriantis nuo įėjimo tik amplitude ir pradine faze; 3) kaip ir signalas, harmoninės funkcijos yra periodinės ir turi begalinę trukmę; 4) harmoninių funkcijų generavimo technika yra gana paprasta.

Iš matematikos kurso žinoma, kad norint išplėsti periodinį signalą į harmoninių funkcijų seriją (2.3), turi būti įvykdytos Dirichlet sąlygos. Tačiau visi tikrieji periodiniai signalai atitinka šias sąlygas ir gali būti pavaizduoti Furjė serijos forma, kurią galima parašyti viena iš šių formų:

u(t) = A 0 / 2+ (A' mn cosnw 1 t + A" mn nw 1 t), (2.4)

kur yra koeficientai

A mn ”= (2.5)

u(t) = A 0 /2+ (2.6)

A mn = (2.7)

arba sudėtinga forma

u(t)= (2.8)

Cn= (2.9)

Iš (2.4) - (2.9) matyti, kad bendruoju atveju periodiniame signale u(t) yra pastovioji dedamoji A 0 /2 ir pagrindinio dažnio w 1 =2pf 1 harmoninių virpesių rinkinys ir jo harmonikų su dažniai w n =nw 1, n=2 ,3,4,… Kiekvienas iš harmonikų

Furjė serijos virpesiams būdinga amplitudė ir pradinė fazė y n .nn

Spektrinė diagrama ir periodinio signalo spektras. Jei kuris nors signalas pateikiamas kaip skirtingų dažnių harmoninių virpesių suma, tada sakoma, kad spektrinis skilimas signalas.

Spektrinė diagrama signalas paprastai vadinamas grafiniu šio signalo Furjė serijos koeficientų atvaizdavimu. Yra amplitudės ir fazių diagramos. Fig. 2.6, tam tikru mastu harmoninių dažnių reikšmės brėžiamos išilgai horizontalios ašies, o jų amplitudės A mn ir fazės y n išilgai vertikalios ašies. Be to, harmoninės amplitudės gali turėti tik teigiamas reikšmes, fazės gali turėti ir teigiamas, ir neigiamas reikšmes intervale -p£y n £p

Signalo spektras- tai harmoninių komponentų rinkinys su konkrečiomis dažnių, amplitudių ir pradinių fazių reikšmėmis, kurios kartu sudaro signalą. IN technines programas praktikoje spektrinės diagramos vadinamos trumpiau - amplitudės spektras, fazių spektras. Dažniausiai žmonės domisi amplitudės spektrine diagrama. Jis gali būti naudojamas norint įvertinti harmonikų procentą spektre.

Pavyzdys 2.3. Išplėskite periodinę stačiakampių vaizdo impulsų seką į Furjė seriją Sužinomi parametrai (U m , T, t z), net "Santykinai su tašku t=0. Sudarykite spektrinę amplitudžių ir fazių diagramą, kai U m =2B, T=20ms, S=T/t ir =2 bei 8.

Nurodytas periodinis signalas vieno periodo intervale gali būti parašytas kaip

Šiam signalui pavaizduoti naudosime Furjė serijos formą V forma (2.4). Kadangi signalas yra tolygus, plėtinyje liks tik kosinuso komponentai.

Ryžiai. 2.6. Periodinio signalo spektrinės diagramos:

a - amplitudė; b- fazė

Nelyginės funkcijos integralas per laikotarpį yra lygus nuliui. Naudodami (2.5) formules randame koeficientus

leidžia mums parašyti Furjė seriją:

Norėdami sukurti konkrečių skaitmeninių duomenų spektrines diagramas, nustatome i=0, 1, 2, 3, ... ir apskaičiuojame harmoninius koeficientus. Pirmųjų aštuonių spektro komponentų skaičiavimo rezultatai apibendrinti lentelėje. 2.1. Serijoje (2.4) A" mn = 0 ir pagal (2.7) A mn =|A' mn |, pagrindinis dažnis f 1 =1/T= 1/20-10 -3 =50 Hz, w 1 =2pf 1 =2p*50=314 rad/s . Amplitudės spektras pav.

2.7 yra sukurta šiems n, kuriame Ir mn daugiau nei 5 % didžiausios vertės.

Iš pateikto 2.3 pavyzdžio matyti, kad didėjant darbo ciklui spektrinių komponentų skaičius didėja, o jų amplitudės mažėja. Teigiama, kad toks signalas turi turtingą spektrą. Pažymėtina, kad daugeliui praktiškai naudojamų signalų nereikia skaičiuoti harmonikų amplitudių ir fazių naudojant anksčiau pateiktas formules.

2.1 lentelė. Periodinės stačiakampių impulsų sekos Furjė eilutės komponentų amplitudės

Ryžiai. 2.7. Periodinės impulsų sekos spektrinės diagramos: A- su darbo ciklu S-2; - b-su darbo ciklu S=8

Matematinėse žinynuose yra Furjė serijos signalų išplėtimo lentelės. Viena iš šių lentelių pateikta priede (A.2 lentelė).

Dažnai kyla klausimas: kiek spektrinių komponentų (harmonikų) reikia paimti, kad Furjė serijoje būtų atvaizduotas tikras signalas? Juk serialas, griežtai tariant, yra begalinis. Čia negalima duoti konkretaus atsakymo. Viskas priklauso nuo signalo formos ir jo atvaizdavimo Furjė serijomis tikslumo. Sklandesnis signalo pasikeitimas – reikia mažiau harmonikų. Jei signalas turi šuolių (nutrūkimų), tada norint pasiekti tą pačią klaidą, reikia susumuoti didesnį harmonikų skaičių. Tačiau daugeliu atvejų, pavyzdžiui, telegrafijoje, manoma, kad stačiakampiams impulsams stačiais frontais perduoti pakanka trijų harmonikų.

Praėjusiame amžiuje Ivanas Bernoulli, Leonardas Euleris ir vėliau Jeanas-Baptiste'as Furjė pirmieji panaudojo periodinių funkcijų vaizdavimą trigonometrinėmis eilutėmis. Šis vaizdavimas pakankamai išsamiai nagrinėjamas kituose kursuose, todėl prisimename tik pagrindinius ryšius ir apibrėžimus.

Kaip minėta aukščiau, bet kokia periodinė funkcija u(t) , kuriai galioja lygybė u(t)=u(t+T) , Kur T=1/F=2p/W , gali būti pavaizduotas Furjė serijoje:

Kiekvieną šios serijos terminą galima išplėsti naudojant dviejų kampų skirtumo kosinuso formulę ir pavaizduoti kaip du terminus:

,

Kur: A n =C n cosφ n, B n =C n sinφ n , Taigi , A

Šansai A n Ir Užeiga nustatomi pagal Eilerio formules:

;
.

At n=0 :

A B 0 =0.

Šansai A n Ir Užeiga , yra vidutinės funkcijos sandaugos vertės u(t) ir harmoninė vibracija su dažniu nw per tam tikrą laikotarpį T . Jau žinome (2.5 skyrius), kad tai yra kryžminės koreliacijos funkcijos, nulemiančios jų ryšio mastą. Todėl koeficientai A n Ir Bn parodykite mums „kiek“ sinuso arba kosinuso bangų dažniu nW esančios šioje funkcijoje u(t) , plečiama Furjė serijoje.

Taigi galime pavaizduoti periodinę funkciją u(t) kaip harmoninių virpesių suma, kur skaičiai Cn yra amplitudės ir skaičiai φn - etapais. Paprastai literatūroje vadinamas amplitudės spektru, ir - fazių spektras. Dažnai atsižvelgiama tik į amplitudės spektrą, kuris vaizduojamas kaip linijos, esančios taškuose nW dažnio ašyje ir turintis skaičių atitinkantį aukštį Cn . Tačiau reikia atsiminti, kad norint gauti vieną su vienu atitikimą tarp laiko funkcijos u(t) o jo spektras turi naudoti ir amplitudės spektrą, ir fazių spektrą. Tai matyti iš to paprastas pavyzdys. Signalai turės tą patį amplitudės spektrą, bet visiškai skirtingo tipo laikinosios funkcijos.

Ne tik periodinė funkcija gali turėti atskirą spektrą. Pavyzdžiui, signalas: nėra periodinis, bet turi atskirą spektrą, susidedantį iš dviejų spektro linijų. Taip pat signalas, susidedantis iš radijo impulsų sekos (impulsai su aukšto dažnio užpildymu), kurių pasikartojimo laikotarpis yra pastovus, bet pradinė aukšto dažnio užpildymo fazė pagal tam tikrą dėsnį skiriasi nuo impulso iki impulso. būti griežtai periodiškai. Tokie signalai vadinami beveik periodiniais. Kaip matysime vėliau, jie taip pat turi atskirą spektrą. Tokių signalų spektrų fizikinę prigimtį tirsime taip pat, kaip ir periodinių.