Sida 1 av 2
Låt oss bestämma ordningen på filtret baserat på de erforderliga förhållandena enligt schemat för dämpning i stoppbandet i boken av G. Lam "Analoga och digitala filter" kap.8.1 s.215.
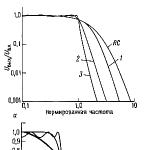
Det är tydligt att ett filter av 4:e ordningen räcker för den erforderliga dämpningen. Grafen visas för fallet när w c \u003d 1 rad / s, och följaktligen är frekvensen vid vilken den nödvändiga dämpningen behövs 2 rad / s (respektive 4 och 8 kHz). Allmän plot för Butterworth filteröverföringsfunktionen:

Vi definierar kretsimplementeringen av filtret:
aktivt fjärde ordningens lågpassfilter med komplex negativ återkoppling:

För att den önskade kretsen ska ha önskat frekvenssvar kan elementen som ingår i den väljas med inte särskilt hög noggrannhet, vilket är ett plus med denna krets.
aktivt lågpassfilter av fjärde ordningen med positiv feedback:

I denna krets måste operationsförstärkarens förstärkning ha ett strikt definierat värde, och förstärkningen för denna krets kommer inte att vara mer än 3. Därför kan denna krets kasseras.
4:e ordningens aktivt lågpassfilter med ohmsk negativ återkoppling

Detta filter är byggt på fyra opamps, vilket ökar bruset och komplexiteten för att beräkna denna krets, så vi kasserar den också.
Från de övervägda scheman väljer vi ett filter med komplex negativ feedback.
Filterberäkning
Definition av överföringsfunktion
Vi skriver tabellvärdena för koefficienterna för Butterworth-filtret av fjärde ordningen:
a 1 \u003d 1,8478 b 1 \u003d 1
a 2 \u003d 0,7654 b 2 \u003d 1
(se W. Titze, K. Schenk "Semiconductor circuitry"-fliken. 13.6 s. 195)
Det allmänna uttrycket för överföringsfunktionen för fjärde ordningens lågpassfilter:

(Se W. Titze, K. Schenk "Semiconductor Circuitry" Tabell 13.2 s. 190 och Form 13.4 s. 186).
Överföringsfunktionen för den första länken har formen:

Överföringsfunktionen för den andra länken har formen:

där wc är filtrets cirkulära frekvens, wc =2pfc.
Beräkning av valörer av delar
Genom att likställa koefficienterna för uttryck (2) och (3) med uttryckskoefficienterna (1), får vi:

Konstanta signalöverföringskoefficienter för kaskader, deras produkt A 0 måste vara lika med 10 enligt tilldelningen. De är negativa, eftersom dessa stadier är inverterande, men deras produkt ger en positiv vinst.
För att beräkna kretsen är det bättre att ställa in kondensatorernas kapacitanser, medan för att värdet på R 2 ska vara giltigt måste villkoret vara uppfyllt
 och motsvarande
och motsvarande 
Baserat på dessa förhållanden väljs C 1 \u003d C 3 \u003d 1 nF, C 2 \u003d 10 nF, C 4 \u003d 33 nF.
Beräkna motståndsvärdena för det första steget:


Motståndsvärdena för det andra steget:


OU val
När du väljer en op-förstärkare är det nödvändigt att ta hänsyn till filtrets frekvensområde: enhetsförstärkningsfrekvensen för op-förstärkaren (där förstärkningen är lika med enhet) måste vara större än produkten av gränsfrekvensen och filterförstärkningen K y.
Eftersom den maximala förstärkningen är 3,33 och gränsfrekvensen är 4 kHz, uppfyller nästan alla existerande op-förstärkare detta villkor.
En annan viktig parameter för en op-förstärkare är dess ingångsimpedans. Den måste vara större än tio gånger kretsmotståndets maximala resistans.
Det maximala motståndet i kretsen är 99,6 kOhm, därför måste ingångsresistansen för op-ampen vara minst 996 kOhm.
Det är också nödvändigt att ta hänsyn till operativsystemets lastkapacitet. För moderna operationsförstärkare är det minsta belastningsmotståndet 2 kOhm. Med tanke på att motstånden R1 och R4 är 33,2 respektive 3,09 kΩ, kommer operationsförstärkarens utgångsström säkert att vara mindre än det maximalt tillåtna.
I enlighet med ovanstående krav väljer vi OU K140UD601 med följande passdata (egenskaper):
K min = 50 000
Rin = 1 MΩ
Frekvenssvaret för Butterworth-filtret beskrivs av ekvationen
Funktioner hos Butterworth-filtret: icke-linjär fasrespons; gränsfrekvens oberoende av antalet poler; oscillerande karaktär av det transienta svaret med en stegvis insignal. När ordningen på filtret ökar, ökar den oscillerande karaktären.
Chebyshev filter
Frekvenssvaret för Chebyshev-filtret beskrivs av ekvationen
 ,
,
var T n 2 (ω/ω n ) är Chebyshev-polynomet n-:e ordningen.
Chebyshev-polynomet beräknas med den rekursiva formeln
Funktioner hos Chebyshev-filtret: ökad PFC-olikformighet; vågig karaktäristik i passbandet. Ju högre filterpassbandsrippel är, desto skarpare är rolloff i övergångsområdet för samma ordning. Den transienta fluktuationen med en stegvis insignal är större än med ett Butterworth-filter. Kvalitetsfaktorn för polerna på Chebyshev-filtret är högre än för Butterworth-filtret.
Bessel filter
Frekvenssvaret för Bessel-filtret beskrivs av ekvationen
 ,
,
var  ;B n 2
(ω/ω
cp h )
är Bessel-polynomet n-:e ordningen.
;B n 2
(ω/ω
cp h )
är Bessel-polynomet n-:e ordningen.
Besselpolynomet beräknas med den rekursiva formeln
Funktioner hos Bessel-filtret: ganska enhetlig frekvensrespons och fasrespons, approximerad av Gauss-funktionen; filtrets fasförskjutning är proportionell mot frekvensen, dvs. Filtret har en frekvensoberoende gruppfördröjning. Gränsfrekvensen ändras när antalet filterpoler ändras. Filtrets frekvensrespons är vanligtvis plattare än Butterworth och Chebyshev. Detta filter är särskilt väl lämpat för impulskretsar och faskänslig signalbehandling.
Cauer filter (ellipsfilter)
Allmän bild av överföringsfunktionen för Cauer-filtret
 .
.
Funktioner hos Cauer-filtret: ojämn frekvensrespons i passbandet och i stoppbandet; den skarpaste nedgången i frekvenssvar av alla ovanstående filter; implementerar de nödvändiga överföringsfunktionerna med en mindre filterordning än när man använder filter av andra typer.
Bestämma filterordningen
Den önskade filterordningen bestäms av formlerna nedan och avrundas till närmaste heltal. Butterworth filterbeställning
 .
.
Beställningen av Chebyshev-filtret
 .
.
För Bessel-filtret finns det ingen formel för beräkning av ordningen, istället ges tabeller som motsvarar ordningen på filtret med minsta nödvändiga avvikelse av fördröjningstiden från enhet vid en given frekvens och förlustnivån i dB).
Vid beräkning av ordningen för Bessel-filtret ställs följande parametrar in:
Procentuell tolerans för gruppfördröjning vid en given frekvens ω ω cp h ;
Dämpningsnivån för filterförstärkningen i dB vid frekvensen kan ställas in. ω , normaliserat med avseende på ω cp h .
Baserat på dessa data bestäms den nödvändiga ordningen för Bessel-filtret.
Schema för lågpassfilterkaskader av 1:a och 2:a ordningen
På fig. 12.4, 12.5 visar typiska scheman för LPF-kaskader.


a) b)
Ris. 12.4. Butterworth, Chebyshev och Bessel LPF-kaskader: en - 1:a ordningen; b - 2:a ordningen


a) b)
Ris. 12.5. Cauer LPF Cascades: en - 1:a ordningen; b - 2:a ordningen
Allmän bild av överföringsfunktionerna för LPF Butterworth, Chebyshev och Bessel av 1:a och 2:a ordningen
 ,
, .
.
Allmän översikt över överföringsfunktionerna för Cauer LPF av 1:a och 2:a ordningen
 ,
,  .
.
Den viktigaste skillnaden mellan 2:a ordningens Cauer-filtret och trapfiltret är att i överföringsfunktionen för Cauer-filtret är frekvensförhållandet Ω s ≠ 1.
Metod för att beräkna LPF för Butterworth, Chebyshev och Bessel
Denna teknik är baserad på koefficienterna i tabellerna och gäller för Butterworth-, Chebyshev- och Bessel-filter. Metoden för att beräkna Cauer-filter ges separat. Beräkningen av LPF för Butterworth, Chebyshev och Bessel börjar med att bestämma deras ordning. För alla filter är parametrarna för lägsta och maximala dämpning och gränsfrekvensen inställda. För Chebyshev-filter bestäms dessutom frekvenssvarsrippeln i passbandet och för Bessel-filter gruppfördröjningen. Därefter bestäms filtrets överföringsfunktion, som kan tas från tabellerna, och dess kaskader av 1:a och 2:a ordningen beräknas, följande beräkningsordning observeras:
Beroende på ordningen och typen av filtret väljs scheman för dess kaskader, medan filtret med jämn ordning består av n/ 2 kaskader av 2:a ordningen, och filtret med udda ordningen är från en kaskad av 1:a ordningen och ( n– 1) / 2 kaskader av 2:a ordningen;
För att beräkna kaskaden av första ordningen:
Värdet bestäms av den valda typen och ordningen på filtret b 1 kaskad av första ordningen;
Genom att minska det upptagna området väljs kapacitansklassificeringen C och beräknade R enligt formeln (du kan välja och R, men det rekommenderas att välja C, av noggrannhetsskäl)
 ;
;
Vinsten beräknas Till på U 1 kaskad av 1:a ordningen, som bestäms av relationen
 ,
,
var Till på Uär förstärkningen av filtret som helhet; Till på U 2 , …, Till på Fn– kaskadförstärkningar av andra ordningen;
Att implementera förstärkning Till på U 1 det är nödvändigt att ställa in motstånden baserat på följande förhållande
R B = R A ּ (Till på U1 –1) .
För att beräkna kaskaden av andra ordningen:
Genom att minska det ockuperade området väljs valörerna av kapacitet C 1 = C 2 = C;
Koefficienterna väljs enligt tabellerna b 1 i och F pi för kaskader av 2:a ordningen;
Enligt det givna värdet på kondensatorer C motstånd beräknas R enligt formeln
 ;
;
För den valda filtertypen måste du ställa in lämplig förstärkning Till på Ui = 3 – (1/F pi) av varje steg av den andra ordningen, genom att ställa in motstånden, baserat på följande förhållande
R B = R A ּ (Till på Ui –1) ;
För Bessel-filter, multiplicera värdena för alla kapacitanser med den erforderliga gruppfördröjningen.
Mycket av teorin bakom digitala IIR-filter (d.v.s. filter för oändliga impulssvar) kräver en förståelse för metoder för design av kontinuerliga tidsfilter. Därför kommer detta avsnitt att tillhandahålla beräkningsformler för flera standardtyper av analoga filter, inklusive Butterworth, Bessel och Chebyshev typ I och II filter. En detaljerad analys av fördelarna och nackdelarna med metoder för att approximera de givna egenskaperna som motsvarar dessa filter finns i ett antal arbeten som ägnas åt metoder för att beräkna analoga filter, så nedan kommer vi bara kortfattat att lista de viktigaste egenskaperna hos filter av varje typ och ge de beräknade förhållanden som är nödvändiga för att erhålla analoga filterkoefficienter.
Låt det vara nödvändigt att beräkna ett normaliserat lågpassfilter med en gränsfrekvens lika med Ω = 1 rad/s. Kvadraten på amplitudkarakteristiken kommer vanligtvis att användas som den approximerade funktionen (undantaget är Bessel-filtret). Vi antar att överföringsfunktionen för det analoga filtret är en rationell funktion av variabeln S i följande form:
Butterworth lågpassfilter kännetecknas av att de har den mest jämna amplitudresponsen vid origo i s-planet. Detta betyder att alla existerande derivator av amplitudkarakteristiken till origo är lika med noll. Kvadraten på amplitudsvaret för ett normaliserat (d.v.s. med en gränsfrekvens på 1 rad/s) Butterworth-filter är:
var n - filterordning. Genom att analytiskt fortsätta funktionen (14.2) till hela S-planet får vi
Alla poler (14.3) är på enhetscirkeln på samma avstånd från varandra i S-plan . Vi uttrycker överföringsfunktionen H(s) genom stolparna i det vänstra halvplanet S :
Var (14.4)
Där k =1,2…..n (14,5)
a k 0 - normaliseringskonstant. Med hjälp av formlerna (14.2) och (14.5) kan vi formulera flera egenskaper hos Butterworth-filter med låg pass.
Egenskaper för Butterworth lågpassfilter:
1. Butterworth-filter har bara poler (alla nollor i överföringsfunktionerna för dessa filter är placerade i oändligheten).
2. Vid en frekvens av Ω=1 rad/s är Butterworth-filterförstärkningen lika (dvs. vid gränsfrekvensen sjunker deras amplitudkarakteristik med 3 dB).
3. Filterordning n definierar hela filtret helt. I praktiken beräknas Butterworth-filtrets ordning vanligtvis från villkoret att tillhandahålla en viss dämpning vid någon given frekvens Ω t > 1. Filterordningen som tillhandahåller vid frekvensen Ω= Ω t< уровень амплитудной характеристики, равный 1/А, можно найти из соотношения
Ris. 14.1. Polarrangemang av ett analogt lågpass Butterworth-filter.
Ris. 14.2- Amplitud- och faskarakteristika, såväl som karaktäristiken för gruppfördröjningen för det analoga lågpass Butterworth-filtret.
Låt t.ex, krävs vid frekvens Ω t = 2 rad/s ge dämpning lika med A = 100. Sedan
Avrundning n upp till ett heltal finner vi att den givna dämpningen ger ett 7:e ordningens Butterworth-filter.
Beslut. Använda som designegenskaper 1/A == 0,0005 (motsvarande en dämpning på 66 dB) och Ω t = 2, vi får n== 10,97. Avrundning ger n = 11. På fig. 14.1 visar arrangemanget av polerna för det beräknade Butterworth-filtret i s-plan. Amplituden (på en logaritmisk skala) och fasegenskaper, såväl som gruppfördröjningskarakteristiken för detta filter, visas i fig. 14.2.
Butterworth filter
Butterworth lågpassfilteröverföringsfunktion n-th order karakteriseras av uttrycket:
Frekvenssvaret för ett Butterworth-filter har följande egenskaper:
1) I valfri ordning n frekvenssvarsvärde
2) vid gränsfrekvensen u=u s
Lågpassfiltrets frekvensgång minskar monotont med ökande frekvens. Av denna anledning kallas Butterworth-filter filter med de mest platta egenskaperna. Figur 3 visar graferna för amplitud-frekvenskarakteristika för Butterworth lågpassfiltret på 1-5 ordningar. Uppenbarligen, ju högre ordningen filtret har, desto mer exakt approximeras frekvenssvaret för ett idealiskt lågpassfilter.

Figur 3 - Frekvenssvar för ett Butterworth lågpassfilter i storleksordningen 1 till 5
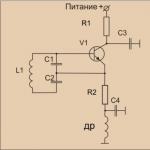
Figur 4 visar en schematisk implementering av Butterworth HPF.

Figur 4 - HPF-II Butterworth
Fördelen med Butterworth-filtret är det jämnaste frekvenssvaret vid passbandsfrekvenser och dess minskning till nästan noll vid undertryckningsbandsfrekvenser. Butterworth-filtret är det enda som bevarar formen på frekvenssvaret för högre ordrar (med undantag för den brantare rolloffen vid cutoff), medan många andra typer av filter (Bessel-filter, Chebyshev-filter, elliptiskt filter) har olika form av frekvenssvaret i olika ordningsföljder.
Jämfört med Chebyshev Type I- och II-filter eller ett elliptiskt filter har Butterworth-filtret en plattare rolloff och måste därför vara av högre ordning (vilket är svårare att implementera) för att ge önskad prestanda vid gränsfrekvenserna.
Chebyshev filter
Kvadraten på modulen för överföringsfunktionen för Chebyshev-filtret ges av:
var är Chebyshev-polynomet. Modulen för överföringsfunktionen för Chebyshev-filtret är lika med en vid de frekvenser där den försvinner.
Chebyshev-filter används vanligtvis där det krävs att ge de erforderliga frekvenssvarsegenskaperna med ett lågordningsfilter, i synnerhet bra frekvensundertryckning från undertryckningsbandet, medan jämnheten i frekvenssvaret vid passband och undertryckningsfrekvenser inte är så viktigt .
Det finns Chebyshev filter I och II släkten.
Chebyshev filter av den första sorten. Detta är en vanligare modifiering av Chebyshev-filter. I passbandet för ett sådant filter är krusningar synliga, vars amplitud bestäms av krusningsindexet e. I fallet med ett analogt elektroniskt Chebyshev-filter är dess ordning lika med antalet reaktiva komponenter som används i dess implementering. En brantare avklingning av karakteristiken kan erhållas om rippel tillåts inte bara i passbandet, utan även i undertryckningsbandet, genom att addera nollor till filtrets överföringsfunktion på den imaginära axeln jsh i det komplexa planet. Detta kommer emellertid att resultera i mindre effektiv undertryckning i undertryckningsbandet. Det resulterande filtret är ett elliptiskt filter, även känt som ett Cauer-filter.
Frekvenssvaret för Chebyshev-lågpassfiltret av fjärde ordningen av det första slaget visas i figur 5.

Figur 5 - Frekvenssvar för Chebyshev lågpassfilter av den första typen av fjärde ordningen
Typ II Chebyshev-filtret (inverterat Chebyshev-filter) används mer sällan än Type I Chebyshev-filtret på grund av den mindre branta rolloffen av amplitudsvaret, vilket leder till en ökning av antalet komponenter. Den har ingen rippel i passbandet, men finns i undertryckningsbandet.
Frekvenssvaret för Chebyshev-lågpassfiltret av den andra typen av fjärde ordningen visas i figur 6.

Figur 6 - Frekvenssvar för Chebyshev lågpassfilter av den andra typen
Figur 7 visar kretsimplementationer av Chebyshev HPF av I- och II-ordningarna.


Figur 7 - Chebyshev HPF: a) Jag beställer; b) II ordning
Egenskaper för frekvensegenskaperna hos Chebyshev-filter:

1) I passbandet har frekvenssvaret en likavågskaraktär. På intervallet (-1? u? 1) finns n punkter där funktionen når ett maximalt värde på 1 eller ett minimivärde på . Om n är udda, om n är jämnt;
2) värdet på frekvenssvaret för Chebyshev-filtret vid gränsfrekvensen är

3) För minskar funktionen monotont och tenderar till noll.
4) Parametern e bestämmer ojämnheten i frekvenssvaret för Chebyshev-filtret i passbandet:
Jämförelse av frekvenssvaret för Butterworth- och Chebyshev-filtren visar att Chebyshev-filtret ger mer dämpning i passbandet än Butterworth-filtret av samma ordning. Nackdelen med Chebyshev-filter är att deras fas-frekvensegenskaper i passbandet skiljer sig avsevärt från linjära.
För Butterworth- och Chebyshev-filter finns det detaljerade tabeller som visar koordinaterna för polerna och koefficienterna för överföringsfunktionerna för olika beställningar.
UKRAINAS UTBILDNINGSMINISTERIE OCH VETENSKAP
Kharkiv National University of Radio Electronics
Institutionen för REU
KURSARBETE
FÖRKÄLLNING OCH FÖRKLARANDE ANM.
SMÖRVÄRT HÖGPASSFILTER
Charkiv 2008
Teknisk uppgift
Konstruera ett högpassfilter (HPF) med approximation av amplitud-frekvenskarakteristiken (AFC) av Butterworth-polynomet, bestäm önskad filterordning om AFC-parametrarna är inställda (Fig. 1): K 0 = 26dB
U m Vx \u003d 250mV
var är den maximala filterförstärkningen;
Minsta vinst i bandbredden;
Maximal filterförstärkning i fördröjningsbandet;
Gränsfrekvens;
Frekvensen från vilken filterförstärkningen är mindre än .

Figur 1 - Butterworth HPF-mall.
Ge en liten känslighet för avvikelser i betygen av elementen.
UPPSATS
Avräkning och förklarande anteckning: 26 s., 11 fig., 6 tab.
Syfte med arbetet: syntes av en aktiv högpass RC-filterkrets och beräkning av dess komponenter.
Forskningsmetod: approximation av filtrets frekvenssvar genom Butterworth-polynomet.
Den ungefärliga överföringsfunktionen implementeras med ett aktivt filter. Filtret är byggt genom att kaskadkoppla oberoende länkar. Aktiva filter använder icke-inverterande förstärkare med finit-gain, som implementeras med hjälp av operationsförstärkare.
Resultaten av arbetet kan användas för att syntetisera filter för radioteknik och hushållsutrustning.
Introduktion
1. Översikt över liknande system
3.1 Implementering av HPF-normalisering
3.2 Bestämma önskad filterordning
3.3 Definition av Butterworth-polynomet
3.4 Omvänd övergång från normaliserad till projicerad HPF
3.5 Övergång från överföringsfunktion till krets
3.6 Övergång från överföringsfunktion till krets
4. Beräkning av kretselement
5. Teknik för att justera det utvecklade filtret
Introduktion
Fram till nyligen kunde resultaten av att jämföra digitala och analoga enheter i radioutrustning och tekniska telekommunikationsmedel inte annat än orsaka en känsla av missnöje. Digitala noder implementerade med den utbredda användningen av integrerade kretsar (IC) skilde sig positivt i sin konstruktiva och tekniska fullständighet. Situationen var annorlunda med noderna för analog signalbehandling, som till exempel inom telekommunikation stod för 40 till 60 % av volymen och massan av kommunikationsutrustning. Skrymmande, innehållande ett stort antal opålitliga och tidskrävande lindningselement, såg de så deprimerande ut mot bakgrund av stora integrerade kretsar att de gav upphov till en åsikt bland ett antal experter om behovet av "total digitalisering" av elektronisk utrustning.
Det senare, liksom alla andra ytterligheter, ledde dock inte (och kunde inte) till resultat som var tillräckliga mot de förväntade. Sanningen, som i alla andra fall, låg någonstans i mitten. I ett antal fall visar sig utrustning byggd på funktionella analoga enheter, vars elementära bas är tillräcklig för mikroelektronikens möjligheter och begränsningar, vara mer effektiv.
Lämpligheten i detta fall kan säkerställas genom övergången till aktiva RC-kretsar, vars elementära bas inte inkluderar induktorer och transformatorer, som i grunden inte implementeras med hjälp av mikroelektronik.
Giltigheten av en sådan övergång bestäms för närvarande, å ena sidan, av prestationerna i teorin om aktiva RC-kretsar, och å andra sidan av framgången med mikroelektronik, som har försett utvecklare med linjära integrerade kretsar av hög kvalitet , inklusive integrerade operationsförstärkare (op-amps). Dessa op-förstärkare, med stor funktionalitet, berikade de analoga kretsarna avsevärt. Detta var särskilt uppenbart i kretsen av aktiva filter.
Fram till 60-talet användes främst passiva element för att implementera filter, d.v.s. induktorer, kondensatorer och motstånd. Huvudproblemet vid implementeringen av sådana filter är storleken på induktorerna (vid låga frekvenser blir de för skrymmande). Med utvecklingen av integrerade operationsförstärkare på 60-talet dök en ny riktning i designen av aktiva filter baserade på op-förstärkare upp. Aktiva filter använder motstånd, kondensatorer och op-amps (aktiva komponenter), men de har inga induktorer. I framtiden ersatte aktiva filter nästan helt passiva. För närvarande används passiva filter endast vid höga frekvenser (över 1 MHz), utanför frekvensområdet för de mest använda op-förstärkarna. Men även i många högfrekventa enheter, såsom radiosändare och mottagare, ersätts traditionella RLC-filter av kvarts- och ytvågsfilter.
Nu ersätts analoga filter i många fall av digitala. Driften av digitala filter tillhandahålls huvudsakligen av programvara, så de är mycket mer flexibla i användning jämfört med analoga. Med hjälp av digitala filter är det möjligt att realisera sådana överföringsfunktioner som är mycket svåra att erhålla med konventionella metoder. Digitala filter kan dock ännu inte ersätta analoga filter i alla situationer, så det finns fortfarande ett behov av de mest populära analoga filtren - aktiva RC-filter.
1. Översikt över liknande system
Filter är frekvensselektiva enheter som skickar eller fördröjer signaler inom vissa frekvensband.
Filter kan klassificeras efter deras frekvenssvar:
1. Lågpassfilter (LPF) - passera alla svängningar med frekvenser som inte är högre än en viss gränsfrekvens och en konstant komponent.
2. Högpassfilter (LPF) - passera alla vibrationer som inte är lägre än en viss gränsfrekvens.
3. Bandpassfilter (BPF) - passoscillationer i ett visst frekvensband, som bestäms av en viss nivå av frekvenssvar.
4. Band-stop filter (BPF) - fördröjning av svängningar i ett visst frekvensband, som bestäms av en viss nivå av frekvenssvar.
5. Notch-filter (RF) - en typ av BPF som har ett smalt fördröjningsband och som även kallas ett stoppfilter.
6. Fasfilter (FF) - har helst en konstant överföringskoefficient vid alla frekvenser och är utformade för att ändra fasen för insignaler (särskilt för signalernas tidsfördröjning).

Figur 1.1 - Huvudtyperna av filter
Med aktiva RC-filter är det omöjligt att uppnå den ideala formen av frekvenssvaret i form av rektanglar som visas i fig. 1.1 med en strikt konstant förstärkning i passbandet, oändlig dämpning i undertryckningsbandet och oändlig branthet i rullningen. av från passband till undertryckningsband. Utformningen av ett aktivt filter är alltid en kompromiss mellan den ideala formen av egenskapen och komplexiteten i dess implementering. Detta kallas "approximationsproblemet". I många fall gör kraven på kvaliteten på filtreringen det möjligt att klara sig med de enklaste filtren av första och andra beställningen. Några scheman för sådana filter presenteras nedan. Filterdesign handlar i det här fallet om att välja en krets med den mest lämpliga konfigurationen och sedan beräkna elementvärdena för specifika frekvenser.
Det finns dock situationer där kraven för filtrering kan vara mycket strängare och system med högre ordning än de första och andra kan krävas. Att designa högklassiga filter är en svårare uppgift, vilket är ämnet för detta kursarbete.
Nedan är några av huvudscheman i den första andra ordningen med en beskrivning av fördelarna och nackdelarna med var och en av dem.
1. LPF-I och HPF-I baserade på en icke-inverterande förstärkare.

Figur 1.2 - Filter baserade på en icke-inverterande förstärkare:
a) LPF-I, b) HPF-I.
Fördelarna med filterkretsar inkluderar främst den enkla implementeringen och inställningen, nackdelarna är den låga brantheten hos frekvensegenskaperna och är inte särskilt motståndskraftiga mot självexcitering.
2. LPF-II och HPF-II med multi-loop återkoppling.

Figur 1.3 - Filter med multi-loop feedback:
a) LPF-II, b) HPF-II.
Tabell 2.1 - För- och nackdelar med LPF-II med multi-loop feedback
Tabell 2.2 - För- och nackdelar med HPF-II med multi-loop feedback
2. LPF-II och HPF-II Sallen-Key.

Figur 1.4 - Sallen-Kay-filter:
a) LPF-II, b) HPF-II
Tabell 2.3 - För- och nackdelar med LPF-II Sallen-Kay.
Tabell 2.4 - För- och nackdelar med Sallen-Kay HPF-II.
3. LPF-II och HPF-II baserade på impedansomvandlare.


Figur 1.5 - LPF II-krets baserad på impedansomvandlare:
a) LPF-II, b) HPF-II.
Tabell 2.3 - För- och nackdelar med LPF-II och HPF-II baserat på impedansomvandlare.
2. Val och motivering av filterschemat
Filterdesignmetoder skiljer sig åt i designfunktioner. Utformningen av passiva RC-filter bestäms till stor del av blockschemat
Aktiva AF-filter beskrivs matematiskt av en överföringsfunktion. Namn på överföringsfunktionspolynom ges till frekvenssvarstyper. Varje typ av frekvensgång är implementerad med ett visst antal poler (RC-kretsar) i enlighet med den specificerade frekvensgången. De mest kända är uppskattningarna av Butterworth, Bessel, Chebyshev.
Butterworth-filtret har det mest platta frekvenssvaret, i undertryckningsbandet är övergångssektionens lutning 6 dB/okt per pol, men det har ett icke-linjärt fassvar, ingångsimpulsspänningen orsakar svängningar vid utgången, därför filter används för kontinuerliga signaler.
Bessel-filtret har ett linjärt fassvar, en liten lutning av övergångssektionen av frekvenssvaret. Signaler av alla frekvenser i passbandet har samma tidsfördröjningar, så det är lämpligt för att filtrera rektangulära pulser som måste skickas utan distorsion.
Chebyshev filter - filter av lika vågor i joint venture, massorna av en platt form utanför den, lämplig för kontinuerliga signaler i fall där lock måste ha en brant lutning av frekvenssvaret bakom gränsfrekvensen.
Enkla filterscheman av första och andra ordningen används endast när det inte finns några strikta krav på kvaliteten på filtreringen.
Kaskadkopplingen av filtersektionerna utförs om filterordningen behövs högre än den andra, det vill säga när det är nödvändigt att bilda en överföringskarakteristik med en mycket stor dämpning av signaler i det undertryckta bandet och en stor lutning på dämpning av frekvenssvaret Den resulterande överföringsfunktionen erhålls genom att multiplicera de partiella överföringskoefficienterna
Kedjor är byggda enligt samma schema, men elementens värden
R, C är olika och beror på gränsfrekvenserna för filtret och dess remsor: f sp.f / f sp.l
Man bör dock komma ihåg att kaskadkoppling av till exempel två andra ordningens Butterworth-filter inte ger ett fjärde ordningens Butterworth-filter, eftersom det resulterande filtret kommer att ha en annan cutoff-frekvens och ett annat frekvenssvar. Därför är det nödvändigt att välja koefficienterna för enstaka länkar på ett sådant sätt att nästa produkt av överföringsfunktionerna motsvarar den valda typen av approximation. Därför kommer utformningen av en AF att orsaka svårigheter när det gäller att få en idealisk egenskap och komplexiteten i dess implementering.
På grund av de mycket stora ingångs- och små utgångsimpedanserna för varje länk, finns det ingen distorsion av den givna överföringsfunktionen och möjligheten till oberoende reglering av varje länk. Länkarnas oberoende gör det möjligt att brett reglera egenskaperna för varje länk genom att ändra dess parametrar.
Det spelar i princip ingen roll i vilken ordning delfiltren placeras, eftersom den resulterande överföringsfunktionen alltid kommer att vara densamma. Det finns dock olika praktiska rekommendationer angående anslutningsordningen för delfilter. Till exempel, för att skydda mot självexcitering, bör en sekvens av länkar organiseras i stigande ordning av den partiella begränsande frekvensen. En annan ordning kan leda till självexcitering av den andra länken i toppområdet för dess frekvenssvar, eftersom filter med högre begränsande frekvenser vanligtvis har en högre kvalitetsfaktor i området för den begränsande frekvensen.
Ett annat kriterium är relaterat till kraven på minimering, ljudnivån vid ingången. I detta fall är sekvensen av länkar omvänd, eftersom filtret med den lägsta gränsfrekvensen dämpar brusnivån som uppstår från de tidigare länkarna i kaskaden.
3. Topologisk filtermodell och spänningsöverföringsfunktion
3.1 I detta stycke kommer ordningen för Butterworth HPF att väljas och typen av dess överföringsfunktion kommer att bestämmas enligt parametrarna som specificeras i ToR:


Figur 2.1 - HPF-mall enligt anvisningarna.
Topologisk filtermodell.

3.2 Genomförande av HPF-normalisering
Enligt tilldelningsvillkoret hittar vi randvillkoren för filterfrekvensen som vi behöver. Och vi normaliserar för överföringskoefficienten och för frekvensen.
Utöver överföringsförhållandet:
K max \u003d K 0 -K p \u003d 26-23 \u003d 3dB
K min \u003d K 0 -K s \u003d 26- (-5) \u003d 31 dB
Efter frekvens:

3.3 Bestämma önskad filterordning

Avrunda n till närmaste heltal: n = 3.
För att uppfylla kraven som ställs av mallen behövs ett tredje ordningens filter.
3.4 Definition av Butterworth-polynomet
Enligt tabellen över normaliserade överföringsfunktioner för Butterworth-filter hittar vi Butterworth-polynomet av tredje ordningen:

3.5 Omvänd övergång från normaliserad till projicerad HPF
Låt oss utföra den omvända övergången från den normaliserade HPF till den projicerade HPF.
skalning med överföringskoefficient:
frekvensskalning:
Vi gör en ersättare
Som ett resultat av skalning får vi överföringsfunktionen W(p) i formen:


Figur 2.2 - Frekvenssvar för den designade HPF Butterworth.
3.6 Övergång från överföringsfunktion till krets
Låt oss representera överföringsfunktionen för den tredje ordningens HPF som är utformad som produkten av överföringsfunktionerna för två aktiva HPF:er av första och andra ordningen, dvs. som
 och
och  ,
,
var är överföringskoefficienten vid en oändligt hög frekvens;
är polens frekvens;
– filtrets kvalitetsfaktor (förhållandet mellan förstärkningen vid frekvensen och förstärkningen i passbandet).
Denna övergång är giltig, eftersom den totala ordningen av seriekopplade aktiva filter kommer att vara lika med summan av beställningarna av individuella filter (1 + 2 = 3).
Den totala filterförstärkningen (K0 = 19,952) kommer att bestämmas av produkten av de individuella filterförstärkningarna (K1, K2).
Om vi utökar överföringsfunktionen till kvadratiska faktorer får vi:

I detta uttryck
![]() . (2.5.1)
. (2.5.1)
Det är lätt att se att polernas frekvenser och kvalitetsfaktorerna för överföringsfunktionerna är olika.
För den första överföringsfunktionen:
polfrekvens ;
kvalitetsfaktorn för HPF-I är konstant och lika med .
För den andra överföringsfunktionen:
polfrekvens ;
kvalitetsfaktor.
För att operationsförstärkarna i varje steg ska ha ungefär lika krav på frekvensegenskaper är det tillrådligt att fördela hela filtrets totala överföringskoefficient mellan vart och ett av stegen i omvänd proportion till kvalitetsfaktorn för motsvarande steg, och välja den karakteristiska frekvensen (enhetsförstärkningsfrekvensen för op-förstärkaren) bland alla steg.
Eftersom HPF i detta fall består av två steg, kan ovanstående villkor skrivas som:
![]()
 . (2.5.2)
. (2.5.2)
Genom att ersätta uttryck (2.5.2) med (2.5.1) får vi:
![]() ;
;
Låt oss kontrollera riktigheten av beräkningen av överföringskoefficienterna. Den totala filtervinsten i tider kommer att bestämmas av produkten av koefficienterna för de individuella filtren. Låt oss översätta koefficienten izdB till tider:
De där. beräkningarna är korrekta.
Låt oss skriva överföringskarakteristiken med hänsyn till värdena som beräknats ovan ():
 .
.
3.7 Välja en tredje ordningens aktiv HPF-krets
Eftersom det enligt uppgiften är nödvändigt att säkerställa en liten känslighet för avvikelser från elementen, kommer vi att välja som det första steget av HPF-I baserat på en icke-inverterande förstärkare (fig. 1.2, b), och andra - HPF-II baserad på impedansomvandlare (CPS), vars krets visas i fig. 1.5, b.
För HPF-I baserad på en icke-inverterande förstärkare är beroendet av filterparametrarna på kretselementens klassificering enligt följande:
För HPF-II baserad på CPS beror filterparametrarna på elementklassificeringen enligt följande:
![]() ; (3.4)
; (3.4)
![]() ;
;
4. Beräkning av kretselement
Beräkning av det första steget (HPF I) med parametrar
Låt oss välja R1 baserat på kraven för ingångsresistansvärdet (): R1 = 200 kOhm. Sedan följer av (3.2) att
![]() .
.
Vi väljer R2 = 10 kOhm, sedan av (3.1) följer det
· Beräkning av den andra kaskaden (HPF II) med parametrar
 . .
. .
Sedan ![]() (koefficienten i täljaren är vald för att erhålla den nominella kapaciteten från standardserien E24). Så C2 = 4,3 nF.
(koefficienten i täljaren är vald för att erhålla den nominella kapaciteten från standardserien E24). Så C2 = 4,3 nF.
Av (3.3) följer att
Av (3.1) följer att
Låt vara  . Så C1 = 36 nF.
. Så C1 = 36 nF.
Tabell 4.1 - Klassificeringar av filterelement
Från data i Tabell 4.1 kan vi börja modellera filterkretsen.
Det gör vi med hjälp av ett specialprogram Workbench5.0.
Schemat och simuleringsresultat visas i figur 4.1. och Fig. 4.2, a-b.

Figur 4.1 - Schema för Butterworth HPF av tredje ordningen.

Figur 4.2 - Resulterande frekvenssvar (a) och fassvar (b) för filtret.
5. Teknik för inställning och reglering av det utvecklade filtret
För att ett riktigt filter ska ge önskad frekvensgång måste resistanser och kapacitanser väljas med stor noggrannhet.
Detta är mycket lätt att göra för motstånd, om de tas med en tolerans på högst 1%, och svårare för kondensatorkapacitet, eftersom de har toleranser i området 5-20%. På grund av detta beräknas kapacitansen först, och sedan beräknas resistansen hos motstånden.
5.1 Välja typ av kondensatorer
Vi kommer att välja den lågfrekventa typen av kondensatorer på grund av deras lägre kostnad.
Kräver små dimensioner och massa kondensatorer
· Det är nödvändigt att välja kondensatorer med så små förluster som möjligt (med en liten dielektrisk förlusttangens).
Några parametrar för K10-17-gruppen (tagna från):
Mått, mm
Vikt, g0,5…2
Tillåten kapacitetsavvikelse, %
Förlust tangent0,0015
Isolationsmotstånd, MOm1000
Drifttemperaturområde – 60…+125
5.2 Välja typ av motstånd
· För kretsen av det designade filtret, för att säkerställa ett lågt temperaturberoende, är det nödvändigt att välja motstånd med en minimal TCR.
· Valda motstånd måste ha en minsta inneboende kapacitans och induktans, så vi kommer att välja en icke-trådstyp av motstånd.
· Emellertid har icke-trådsmotstånd en högre nivå av strömbrus, så parametern för motståndens egenbrusnivå måste också beaktas.
Precisionsmotstånd av typ C2-29V uppfyller de specificerade kraven (parametrarna är hämtade från):
Märkeffekt, W 0,125;
Nominellt motståndsområde, Ohm;
TCS (i temperaturområdet),
TCS (i temperaturområdet ![]() ),
),
Självljudnivå, µV/V1…5
Begränsa driftspänningen DC
och växelström, V200
5.3 Välja typ av operationsförstärkare
· Huvudkriteriet för att välja en op-förstärkare är dess frekvensegenskaper, eftersom riktiga op-förstärkare har en ändlig bandbredd. För att frekvensegenskaperna för op-förstärkaren inte ska påverka karakteristiken för det designade filtret, är det nödvändigt att för enhetsförstärkningsfrekvensen för op-förstärkaren i det i-te steget är förhållandet uppfyllt:
För den första kaskaden: .
För den andra kaskaden: .
Genom att välja ett högre värde får vi att enhetsförstärkningsfrekvensen för op-förstärkaren inte bör vara mindre än 100 kHz.
Förstärkningen på op-amp måste vara tillräckligt stor.
· Matningsspänningen för op-förstärkaren måste matcha spänningen för strömförsörjningen, om den är känd. Annars är det önskvärt att välja en op-amp med ett brett utbud av matningsspänningar.
· När du väljer en op-amp för ett flerstegs högpassfilter är det bättre att välja en op-amp med lägsta möjliga förspänning.
Enligt referensboken kommer vi att välja ett OS av typ 140UD6A, strukturellt utformat i ett fall av typ 301.8-2. Op-amps av denna typ är generella op-amps med intern frekvenskorrigering och utgångsskydd i händelse av belastningskortslutning och har följande parametrar:
Matningsspänning, V
Matningsspänning, V
Förbrukningsström, mA
Förspänning, mV
Op-amp spänningsförstärkning
Enhetsförstärkningsfrekvens, MHz1
5.4 Teknik för inställning och justering av det utvecklade filtret
Att ställa in detta filter är inte särskilt svårt. Frekvenssvarsparametrarna "justeras" med hjälp av motstånd, både det första och andra steget, oberoende av varandra, och inställningen av en filterparameter påverkar inte värdena för andra parametrar.
Inställningen görs enligt följande:
1. Förstärkningen ställs in av motstånden R2 i det första och R5 i det andra steget.
2. Frekvensen för polen för det första steget ställs in av motståndet R1, frekvensen för polen för det andra steget ställs in av motståndet R4.
3. Kvalitetsfaktorn för det andra steget regleras av motståndet R8, och kvalitetsfaktorn för det första steget regleras inte (den är konstant för alla betyg av elementen).
Resultatet av detta kursarbete är att erhålla och beräkna schemat för ett givet filter. HPF med approximation av frekvensegenskaperna av Butterworth-polynomet med parametrarna som anges i referensvillkoren, har en tredje ordningen och är en tvåstegsansluten HPF av första ordningen (baserat på en icke-inverterande förstärkare) andra ordningen (baserat på impedansomvandlare). Kretsen innehåller tre operationsförstärkare, åtta motstånd och tre kapacitanser. Denna krets använder två nätaggregat på 15 V vardera.
Valet av krets för varje steg i det gemensamma filtret utfördes på grundval av den tekniska uppgiften (för att säkerställa låg känslighet för avvikelser i elementens värden), med hänsyn till fördelarna och nackdelarna med varje typ av filter kretsar som används som stegen i det gemensamma filtret.
Värdena för kretselementen valdes och beräknades på ett sådant sätt att de förde dem så nära standardserien E24 som möjligt, och även för att erhålla största möjliga ingångsimpedans för varje filtersteg.
Efter modellering av filterkretsen med hjälp av ElectronicsWorkbench5.0-paketet (Fig. 5.1), erhölls frekvenssvar (Fig. 5.2) med de erforderliga parametrarna som anges i referensvillkoren (Fig. 2.2).
Fördelarna med detta schema inkluderar enkelheten att ställa in alla filterparametrar, oberoende inställning av varje steg separat och låg känslighet för avvikelser från elementvärdena.
Nackdelarna är användningen av tre operationsförstärkare i filterkretsen och följaktligen dess ökade kostnad, samt en relativt låg ingångsimpedans (ca 50 kOhm).
Lista över begagnad litteratur
1. Zelenin A.N., Kostromitsky A.I., Bondar D.V. – Aktiva filter på operationsförstärkare. - Kh .: Teletekh, 2001. utg. för det andra, korrekt. och ytterligare - 150 s.: ill.
2. Motstånd, kondensatorer, transformatorer, drossel, REA-omkopplingsanordningar: Ref./N.N. Akimov, E.P. Vashchukov, V.A. Prokhorenko, Yu.P. Khodorenok. - Minsk: Vitryssland, 2004. - 591 s.: ill.
Analoga integrerade kretsar: Ref./A.L. Bulychev, V.I. Galkin, 382 s.: V.A. Prokhorenko. - 2:a uppl., reviderad. och ytterligare - Minsk: Vitryssland, 1993. - helvete.