Planen:

Introduktion

• 1 Översikt
  • 1.1 Normaliserade Butterworth-polynom
  • 1.2 Maximal jämnhet
  • 1.3 Rolloff vid höga frekvenser
• 2 Filterdesign
  • 2.1 Cauer topologi
  • 2.2 Sallen-Kay topologi
• 3 Jämförelse med andra linjära filter
• 4 Exempel
Litteratur

Introduktion

Butterworth filter- en av typerna av elektroniska filter. Filter av denna klass skiljer sig från andra genom designmetoden. Butterworth-filtret är utformat så att dess frekvenssvar är så jämnt som möjligt vid passbandsfrekvenser.

Sådana filter beskrevs först av den brittiske ingenjören Stephen Butterworth i hans artikel On the Theory of Filter Amplifiers. Om teorin om filterförstärkare ), i journalen Trådlös ingenjörår 1930.

1. Översikt

Frekvenssvaret för Butterworth-filtret är så jämnt som möjligt vid passbandsfrekvenserna och sjunker till nästan noll vid undertryckningsfrekvenserna. När frekvenssvaret för ett Butterworth-filter visas på ett logaritmiskt fassvar, minskar amplituden mot minus oändlighet vid gränsfrekvenserna. I fallet med ett första ordningens filter avtar frekvensgången med en hastighet av −6 decibel per oktav (-20 decibel per decennium) (i själva verket är alla första ordningens filter, oavsett typ, identiska och har samma frekvenssvar). För ett andra ordningens Butterworth-filter dämpas frekvensgången med -12 dB per oktav, för ett tredje ordningens filter med -18 dB, och så vidare. Frekvenssvaret för Butterworth-filtret är en monotont minskande funktion av frekvensen. Butterworth-filtret är det enda filtret som bevarar formen på frekvenssvaret för högre beställningar (med undantag för en brantare rolloff i avvisningsbandet), medan många andra filtervarianter (Bessel-filter, Chebyshev-filter, elliptiskt filter) har olika form av frekvenssvaret i olika ordningsföljder.

Jämfört med Chebyshev Typ I- och II-filter eller ett elliptiskt filter har Butterworth-filtret en plattare rolloff och måste därför vara av högre ordning (vilket är svårare att implementera) för att ge önskad prestanda vid gränsfrekvenserna. Butterworth-filtret har dock ett mer linjärt fassvar vid passbandsfrekvenser.

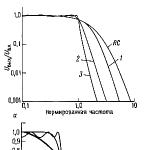
Frekvenssvar för Butterworth lågpassfilter i storleksordningen 1 till 5. Lutningen på karakteristiken är 20 n dB/decennium, var n- filterordning.

Som med alla filter, när man överväger frekvensegenskaperna, används ett lågpassfilter, från vilket det är lätt att få ett högpassfilter, och, genom att inkludera flera sådana filter i serie, ett bandpassfilter eller en skåra filtrera.

Frekvenssvaret för ett th-orders Butterworth-filter kan erhållas från överföringsfunktionen:

Det är lätt att se att för oändliga värden blir frekvenssvaret en rektangulär funktion, och frekvenser under gränsfrekvensen kommer att passeras igenom med en förstärkning, medan frekvenser över gränsfrekvensen kommer att undertryckas helt. För ändliga värden kommer sönderfallet av egenskapen att vara mild.

Med hjälp av en formell substitution representerar vi uttrycket i formen:

Överföringsfunktionens poler är placerade på en cirkel med radie på samma avstånd från varandra i det vänstra halvplanet. Det vill säga, överföringsfunktionen för ett Butterworth-filter kan endast bestämmas genom att bestämma polerna för dess överföringsfunktion i det vänstra halvplanet av s-planet. -:e polen bestäms av följande uttryck:

Överföringsfunktionen kan skrivas som:

Liknande överväganden gäller digitala Butterworth-filter, med den enda skillnaden som förhållandena inte är skrivna för s-plan, och för z-plan.

Nämnaren för denna överföringsfunktion kallas Butterworth-polynomet.

1.1. Normaliserade Butterworth-polynom

Butterworthpolynom kan skrivas i komplex form som visas ovan, men de skrivs vanligtvis som förhållanden med reella koefficienter (komplexa konjugerade par kombineras med multiplikation). Polynom normaliseras med gränsfrekvensen: . De normaliserade Butterworth-polynomen har alltså följande kanoniska form:

, - jämn , - udda

Nedan är koefficienterna för Butterworth-polynomen för de första åtta ordningarna:

Polynomkoefficienter 1 2 3 4 5 6 7 8

1.2. Maximal jämnhet

Att ta och , derivatan av amplitudkarakteristiken med avseende på frekvens kommer att se ut så här:

Den minskar monotont för alla eftersom vinsten alltid är positiv. Sålunda har Butterworth-filtrets frekvenssvar ingen rippel. När vi utökar amplitudkarakteristiken i en serie får vi:

Med andra ord, alla derivator av amplitud-frekvenskarakteristiken med avseende på frekvens upp till 2 n-th är lika med noll, vilket innebär "maximal jämnhet".

1.3. Rolloff vid höga frekvenser

Efter att ha accepterat hittar vi lutningen på logaritmen för frekvenssvaret vid höga frekvenser:

I decibel har den högfrekventa asymptoten en lutning på -20 n dB/decennium.

2. Filterdesign

Det finns ett antal olika filtertopologier som implementerar linjära analoga filter. Dessa scheman skiljer sig endast i elementens värden, strukturen förblir oförändrad.

2.1. Cauer topologi

Cauer-topologin använder passiva element (kapacitanser och induktanser). Ett Butteworth-filter med en given överföringsfunktion kan konstrueras i form av en Type 1 Cauer. Filtrets k:te element ges av relationen:

; k är udda; k är jämnt

2.2. Sallen-Kay topologi

Sallen-Kay-topologin använder, förutom passiva element, aktiva element (op-förstärkare och kondensatorer). Varje steg i Sallen-Kay-kretsen är en del av filtret, matematiskt beskrivet av ett par komplexa konjugerade poler. Hela filtret erhålls genom att seriekoppla alla steg. Om en riktig stolpe stöter på, måste den implementeras separat, vanligtvis i form av en RC-kedja, och inkluderas i den övergripande kretsen.

Överföringsfunktionen för varje steg i Sallen-Kay-schemat är:

Nämnaren måste vara en av faktorerna i Butterworth-polynomet. Med , får vi:

Den sista relationen ger två okända, som kan väljas godtyckligt.

3. Jämförelse med andra linjära filter

Bilden nedan visar frekvenssvaret för Butterworth-filtret jämfört med andra populära linjära filter av samma (femte) ordning:

Det kan ses av figuren att Butterworth-filtret har den långsammaste roll-off av de fyra, men det har också det jämnaste frekvenssvaret vid passbandsfrekvenser.

4. Exempel

Analogt lågpass Butterworth-filter (Cauer-topologi) med en gränsfrekvens med följande elementvärden: farad, ohm och henry.

Logaritmisk plot av överföringsfunktionens densitet H(s) på det komplexa argumentplanet för ett tredje ordningens Butterworth-filter med gränsfrekvens . De tre polerna ligger på en cirkel med enhetsradie i det vänstra halvplanet.

Överväg ett tredje ordningens analogt lågpass Butterworth-filter med farad, ohm och henry. Betecknar impedansen för kapacitanserna C som 1/Cs och impedans för induktorer L som Ls, där är en komplex variabel, och med hjälp av ekvationerna för att beräkna elektriska kretsar får vi följande överföringsfunktion för ett sådant filter:

Frekvenssvaret ges av ekvationen:

och PFC ges av ekvationen:

Gruppfördröjning definieras som minus derivatan av fasen med avseende på den cirkulära frekvensen och är ett mått på fasdistorsionen hos en signal vid olika frekvenser. Det logaritmiska frekvenssvaret för ett sådant filter har ingen rippel vare sig i passbandet eller i undertryckningsbandet.

Diagrammet av modulen för överföringsfunktionen i det komplexa planet indikerar tydligt tre poler i det vänstra halvplanet. Överföringsfunktionen bestäms helt av läget för dessa poler på enhetscirkeln symmetriskt kring den verkliga axeln.

Genom att ersätta varje induktans med en kapacitans, och kapacitanserna med induktanser, får vi ett Butterworth högpassfilter.

Och gruppfördröjningen av ett tredje ordningens Butterworth-filter med en cutoff-frekvens

Litteratur

• V.A. Lucas Teori om automatisk kontroll. - M.: Nedra, 1990.
• B.H. Krivitsky Uppslagsbok om radioelektronikens teoretiska grunder. - M .: Energi, 1977.
• Miroslav D. Lutovac Filterdesign för signalbehandling med MATLAB© och Mathematica©. - New Jersey, USA.: Prentice Hall, 2001. - ISBN 0-201-36130-2
• Richard W Daniels Approximationsmetoder för elektronisk filterdesign. - New York: McGraw-Hill, 1974. - ISBN 0-07-015308-6
• Steven W. Smith Vetenskapsmannens och ingenjörens guide till digital signalbehandling. -Andra upplagan. - San Diego: California Technical Publishing, 1999. - ISBN 0-9660176-4-1
• Britton C. Rorabaugh Approximationsmetoder för elektronisk filterdesign. - New York: McGraw-Hill, 1999. - ISBN 0-07-054004-7
• B. Widrow, S.D. Stearns Adaptiv signalbehandling. - Paramus, NJ: Prentice-Hall, 1985. - ISBN 0-13-004029-0
• S. Haykin Adaptiv filterteori. - 4:e upplagan. - Paramus, NJ: Prentice-Hall, 2001. - ISBN 0-13-090126-1
• Michael L. Honig, David G. Messerschmitt Adaptiva filter – strukturer, algoritmer och applikationer. - Hingham, MA: Kluwer Academic Publishers, 1984. - ISBN 0-89838-163-0
• J.D. Markel, A.H. Grey, Jr. Linjär förutsägelse av tal. - New York: Springer-Verlag, 1982. - ISBN 0-387-07563-1
• L.R. Rabiner, R.W. Schafer Digital bearbetning av talsignaler. - Paramus, NJ: Prentice-Hall, 1978. - ISBN 0-13-213603-1
• Richard J Higgins Digital signalbehandling i VLSI. - Paramus, NJ: Prentice-Hall, 1990. - ISBN 0-13-212887-X
• A.V. Oppenheim, R.W. Schafer Digital signalbehandling. - Paramus, NJ: Prentice-Hall, 1975. - ISBN 0-13-214635-5
• L. R. Rabiner, B. Gold Teori och tillämpning av digital signalbehandling. - Paramus, NJ: Prentice-Hall, 1986. - ISBN 0-13-914101-4
• John G. Proakis, Dimitris G. Manolakis Introduktion till digital signalbehandling. - Paramus, NJ: Prentice-Hall, 1988. - ISBN 0-02-396815-X

När man analyserar filter och beräknar deras parametrar används alltid vissa standardtermer och det är vettigt att hålla sig till dem från första början.

Låt oss anta att det krävs ett lågpassfilter med platt respons i passbandet och en skarp övergång till avvisningsbandet. Den slutliga lutningen för svaret i stoppbandet kommer alltid att vara 6n dB/oktav, där n är antalet "poler". En kondensator (eller induktor) behövs per pol, så kraven på filtrets slutliga avrullningshastighet avgör grovt sett dess komplexitet.

Låt oss nu säga att du bestämmer dig för att använda ett 6-poligt lågpassfilter. Du är garanterad en slutlig rolloff på 36 dB/oktav vid höga frekvenser. I sin tur är det nu möjligt att optimera filterkretsen i betydelsen att tillhandahålla det mest platta svaret i passbandet genom att reducera brantheten i övergången från passbandet till stoppbandet. Å andra sidan, genom att tillåta viss passbandsrippel, kan en brantare övergång från passband till stoppband uppnås. Det tredje kriteriet, som kan vara viktigt, beskriver filtrets förmåga att passera signaler med ett spektrum som ligger i passbandet utan förvrängning av deras form orsakad av fasförskjutningar. Du kan också vara intresserad av stigtid, överskjutning och avvecklingstid.

Filterdesigntekniker är kända som är lämpliga för att optimera vilken som helst av dessa egenskaper eller kombinationer därav. Riktigt vettigt filterval sker inte som beskrivits ovan; i regel ställs först den erforderliga likformigheten hos karakteristiken i passbandet och den erforderliga dämpningen vid en viss frekvens utanför passbandet och andra parametrar. Därefter väljs den mest lämpliga kretsen med det antal poler som är tillräckligt för att uppfylla alla dessa krav. De kommande avsnitten kommer att titta på de tre mest populära typerna av filter, nämligen Butterworth-filtret (maximalt platt svar i passbandet), Chebyshev-filtret (brantaste övergången från passband till stoppband) och Bessel-filtret (maximal platt svarstidsfördröjning) ). Vilken som helst av dessa filtertyper kan implementeras med hjälp av olika filterscheman; vi kommer att diskutera några av dem senare.Alla är lika lämpliga för att bygga lågpass-, högpass- och bandpassfilter.

Butterworth och Chebyshev filter. Butterworth-filtret ger det mest platta svaret i passbandet, vilket uppnås till bekostnad av jämn respons i övergångsregionen, dvs. mellan pass- och stoppband. Som kommer att visas senare har den också en dålig fasrespons. Dess frekvenssvar ges av följande formel:
U ut / U in = 1/1/2,
där n anger filterordningen (antal poler). Att öka antalet poler gör det möjligt att platta ut sektionen av karakteristiken i passbandet och öka brantheten av avklingningen från passbandet till undertryckningsbandet, som visas i fig. 5.10.

Ris. 5.10 Normaliserade egenskaper hos Butterworth lågpassfilter. Notera ökningen av lutningen av rolloff när filterordningen ökar.

Genom att välja ett Butterworth-filter offrar vi allt annat för att få den mest platta responsen. Dess karakteristik går horisontellt, med början från noll frekvens, dess böjning börjar vid gränsfrekvensen ƒ s - denna frekvens motsvarar vanligtvis -3 dB-punkten.

I de flesta applikationer är den viktigaste faktorn att passbandsrippeln inte får överstiga en viss mängd, säg 1 dB. Chebyshev-filtret uppfyller detta krav, medan en viss ojämnhet av karakteristiken är tillåten i hela passbandet, men skärpan i dess brott ökar kraftigt. För Chebyshev-filtret anges antalet poler och passbandsrippel. Om vi ​​antar en ökning av passbandsrippel, får vi en skarpare kink. Frekvenssvaret för detta filter ges av följande samband
U ut / U in = 1/1/2,
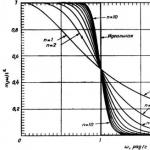
där C n är ett Chebyshev-polynom av den första typen av grad n, och ε är en konstant som bestämmer olikformigheten för karakteristiken i passbandet. Chebyshev-filtret, liksom Butterworth-filtret, har fasfrekvensegenskaper som är långt ifrån idealiska. På fig. Figur 5.11 visar för jämförelse egenskaperna hos de 6-poliga lågpassfiltren i Chebyshev och Butterworth. Som du kan se är båda mycket bättre än det 6-poliga RC-filtret.

Ris. 5.11. Jämförelse av egenskaper hos några vanliga 6-poliga lågpassfilter. Egenskaperna för samma filter visas i både logaritmiska (översta) och linjära (botten) skalor. 1 - Bessel-filter; 2 - Butterworth-filter; 3 - Chebyshev-filter (rippel 0,5 dB).

Faktum är att ett Butterworth-filter med det mest platta svaret i passbandet inte är så attraktivt som det kan verka, eftersom du i alla fall måste stå ut med lite passband-rippel (för ett Butterworth-filter kommer detta att vara en gradvis minskning av svaret när du närmar dig frekvensen ƒ s, och för Chebyshev-filtret - krusningar fördelade över hela passbandet). Dessutom kommer aktiva filter byggda av element vars värden har viss tolerans att ha en egenskap som skiljer sig från den beräknade, vilket innebär att det i verkligheten alltid kommer att finnas någon passbandsrippel på Butterworth-filterkarakteristiken. På fig. 5.12 illustrerar inverkan av de mest oönskade avvikelserna i värdena för kondensatorns kapacitans och motståndet på motståndet på filterkarakteristiken.

Ris. 5.12. Inverkan av förändringar i parametrarna för elementen på egenskaperna hos det aktiva filtret.

Mot bakgrund av ovanstående är Chebyshev-filtret en mycket rationell struktur. Det hänvisas ibland till som ett filter med lika våglängd, eftersom dess karaktäristik i övergångsområdet har en stor branthet på grund av det faktum att flera lika stora rippel är fördelade över passbandet, vars antal ökar med filterordningen. Även med relativt små krusningar (i storleksordningen 0,1 dB) ger Chebyshev-filtret en mycket större lutning i övergångsområdet än Butterworth-filtret. För att kvantifiera denna skillnad, anta att du vill ha ett filter med passbandsrippel mindre än 0,1 dB och dämpning på 20 dB vid en frekvens som är 25 % bort från passbandets gränsfrekvens. Beräkningen visar att i det här fallet krävs ett 19-poligt Butterworth-filter, eller endast ett 8-poligt Chebyshev-filter.

Tanken att man kan stå ut med rippel i passbandet för att öka brantheten i övergångssektionen förs till sin logiska slutsats i idén om det så kallade elliptiska filtret (eller Cauer-filtret), där rippel i karakteristiken tillåts både i passbandet och i bandfördröjningen för att säkerställa att övergångssektionens branthet är ännu större än Chebyshev-filterkarakteristiken. Med hjälp av en dator är det möjligt att designa elliptiska filter lika enkelt som klassiska Chebyshev- och Butterworth-filter. På fig. 5.13 är en grafisk uppgift för filtrets amplitud-frekvenskarakteristik. I det här fallet (lågpassfilter), det tillåtna filterförstärkningsområdet (d.v.s. rippel) i passbandet, den lägsta frekvensen vid vilken karakteristiken lämnar passbandet, den maximala frekvensen vid vilken karakteristiken går in i stoppbandet och den lägsta dämpningen i passbandet bestäms kvarhållande.

Ris. 5.13. Ställer in filtrets frekvenssvarsparametrar.

Bessel filter. Som det fastställdes tidigare ger filtrets amplitudfrekvenskarakteristik inte fullständig information om det. Ett filter med platt frekvenssvar kan ha stora fasförskjutningar. Som ett resultat kommer formen på signalen, vars spektrum ligger i passbandet, att förvrängas när den passerar genom filtret. I en situation där vågformen är av största vikt är det önskvärt att ha ett linjärt fasfilter (filter med konstant fördröjningstid) tillgängligt. Att kräva ett filter för att säkerställa att fasförskjutningen ändras linjärt med frekvensen är ekvivalent med att kräva en konstant fördröjningstid för en signal vars spektrum är beläget i passbandet, dvs. frånvaron av vågformsdistorsion. Bessel-filtret (även kallat Thomson-filtret) har den flataste delen av passbandslatenskurvan, precis som Butterworth-filtret har det flataste frekvenssvaret. För att förstå förbättringen i tidsdomänen som Bessel-filtret ger, titta på Fig. 5.14, som visar frekvensnormaliserade fördröjningstidsdiagram för 6-poliga Bessel och Butterworth lågpassfilter. Butterworth-filtrets dåliga fördröjningstid gör att effekter av glitch-typ uppstår när pulsade signaler passerar genom filtret. Å andra sidan måste Bessel-filtret betala för fördröjningstidernas beständighet genom att dess amplitud-frekvenskarakteristik har en ännu plattare övergångssektion mellan pass- och stoppbanden än till och med Butterworth-filterkarakteristiken.

Ris. 5.14. Jämförelse av tidsfördröjningar för 6-bands Bessel (1) och Butterworth (2) lågpassfilter. Bessel-filtret ger, på grund av dess utmärkta egenskaper i tidsdomänen, minst vågformsförvrängning.

Det finns många olika sätt att designa filter som försöker förbättra prestandan hos ett Bessel-filter i tidsdomänen, och delvis offra latenskonstans för att minska stigtiden och förbättra frekvensresponsen. Gaussfiltret har nästan lika bra fasrespons som Bessel-filtret, men med förbättrad transientrespons. En annan intressant klass är filter som gör det möjligt att uppnå identiska krusningar i fördröjningstidskurvan i passbandet (liknande krusningarna i Chebyshev-filtrets amplitud-frekvenskarakteristik) och ger ungefär samma fördröjning för signaler med ett spektrum upp till stoppbandet . Ett annat tillvägagångssätt för att skapa filter med en konstant fördröjningstid är användningen av genomgående filter, annars kallade utjämnare i tidsdomänen. Dessa filter har ett konstant frekvenssvar och fasförskjutningen kan ändras enligt specifika krav. Således kan de användas för att utjämna fördröjningstiden för alla filter, i synnerhet Butterworth- och Chebyshev-filter.

Jämförelse av filter. Trots tidigare kommentarer om stegresponsen för Bessel-filter har det fortfarande mycket bra tidsdomänegenskaper jämfört med Butterworth- och Chebyshev-filter. Själva Chebyshev-filtret, med sin mycket lämpliga frekvensrespons, har den sämsta tidsdomänprestandan av alla tre av dessa filtertyper. Butterworth-filtret erbjuder en kompromiss mellan frekvenser och timing. På fig. Figur 5.15 ger information om prestandan för dessa tre typer av filter i tidsdomänen, förutom de frekvenssvarsdiagram som visats tidigare. Baserat på dessa data kan vi dra slutsatsen att i de fall där filterparametrarna i tidsdomänen är viktiga är det önskvärt att använda Bessel-filtret.

Ris. 5.15. Jämförelse av transienter för 6-poliga lågpassfilter. Kurvorna normaliseras genom att konvertera ett dämpningsvärde på 3 dB till en frekvens på 1 Hz. 1 - Bessel-filter; 2 - Butterworth-filter; 3 - Chebyshev-filter (rippel 0,5 dB).

Frekvenssvaret för Butterworth-filtret beskrivs av ekvationen

Funktioner hos Butterworth-filtret: icke-linjär fasrespons; gränsfrekvens oberoende av antalet poler; oscillerande karaktär av det transienta svaret med en stegvis insignal. När ordningen på filtret ökar, ökar den oscillerande karaktären.

Chebyshev filter

Frekvenssvaret för Chebyshev-filtret beskrivs av ekvationen

,

var T n 2 (ω/ω n ) är Chebyshev-polynomet n-:e ordningen.

Chebyshev-polynomet beräknas med den rekursiva formeln

Funktioner hos Chebyshev-filtret: ökad PFC-olikformighet; vågig karaktäristik i passbandet. Ju högre filterpassbandsrippel är, desto skarpare är rolloff i övergångsområdet för samma ordning. Den transienta fluktuationen med en stegvis insignal är större än med ett Butterworth-filter. Kvalitetsfaktorn för polerna på Chebyshev-filtret är högre än för Butterworth-filtret.

Bessel filter

Frekvenssvaret för Bessel-filtret beskrivs av ekvationen

,

var
;B n 2 (ω/ω cp h ) är Bessel-polynomet n-:e ordningen.

Besselpolynomet beräknas med den rekursiva formeln

Funktioner hos Bessel-filtret: ganska enhetlig frekvensrespons och fasrespons, approximerad av Gauss-funktionen; filtrets fasförskjutning är proportionell mot frekvensen, dvs. Filtret har en frekvensoberoende gruppfördröjning. Gränsfrekvensen ändras när antalet filterpoler ändras. Filtrets frekvensrespons är vanligtvis plattare än Butterworth och Chebyshev. Detta filter är särskilt väl lämpat för impulskretsar och faskänslig signalbehandling.

Cauer filter (ellipsfilter)

Allmän bild av överföringsfunktionen för Cauer-filtret

.

Funktioner hos Cauer-filtret: ojämn frekvensrespons i passbandet och i stoppbandet; den skarpaste nedgången i frekvenssvar av alla ovanstående filter; implementerar de nödvändiga överföringsfunktionerna med en mindre filterordning än när man använder filter av andra typer.

Bestämma filterordningen

Den önskade filterordningen bestäms av formlerna nedan och avrundas till närmaste heltal. Butterworth filterbeställning

.

Beställningen av Chebyshev-filtret

.

För Bessel-filtret finns det ingen formel för beräkning av ordningen, istället ges tabeller som motsvarar ordningen på filtret med minsta nödvändiga avvikelse av fördröjningstiden från enhet vid en given frekvens och förlustnivån i dB).

Vid beräkning av ordningen för Bessel-filtret ställs följande parametrar in:

Procentuell tolerans för gruppfördröjning vid en given frekvens ω ω cp h ;

Dämpningsnivån för filterförstärkningen i dB vid frekvensen kan ställas in. ω , normaliserat med avseende på ω cp h .

Baserat på dessa data bestäms den nödvändiga ordningen för Bessel-filtret.

Schema för lågpassfilterkaskader av 1:a och 2:a ordningen

På fig. 12.4, 12.5 visar typiska scheman för LPF-kaskader.

a) b)

Ris. 12.4. Butterworth, Chebyshev och Bessel LPF-kaskader: en - 1:a ordningen; b - 2:a ordningen

a) b)

Ris. 12.5. Cauer LPF Cascades: en - 1:a ordningen; b - 2:a ordningen

Allmän bild av överföringsfunktionerna för LPF Butterworth, Chebyshev och Bessel av 1:a och 2:a ordningen

,
.

Allmän översikt över överföringsfunktionerna för Cauer LPF av 1:a och 2:a ordningen

,
.

Den viktigaste skillnaden mellan 2:a ordningens Cauer-filtret och trapfiltret är att i överföringsfunktionen för Cauer-filtret är frekvensförhållandet Ω s ≠ 1.

Metod för att beräkna LPF för Butterworth, Chebyshev och Bessel

Denna teknik är baserad på koefficienterna i tabellerna och gäller för Butterworth-, Chebyshev- och Bessel-filter. Metoden för att beräkna Cauer-filter ges separat. Beräkningen av LPF för Butterworth, Chebyshev och Bessel börjar med att bestämma deras ordning. För alla filter är parametrarna för lägsta och maximala dämpning och gränsfrekvensen inställda. För Chebyshev-filter bestäms dessutom frekvenssvarsrippeln i passbandet och för Bessel-filter gruppfördröjningen. Därefter bestäms filtrets överföringsfunktion, som kan tas från tabellerna, och dess kaskader av 1:a och 2:a ordningen beräknas, följande beräkningsordning observeras:

Beroende på ordningen och typen av filtret väljs scheman för dess kaskader, medan filtret med jämn ordning består av n/ 2 kaskader av 2:a ordningen, och filtret med udda ordningen är från en kaskad av 1:a ordningen och ( n– 1) / 2 kaskader av 2:a ordningen;

För att beräkna kaskaden av första ordningen:

Värdet bestäms av den valda typen och ordningen på filtret b 1 kaskad av första ordningen;

Genom att minska det upptagna området väljs kapacitansklassificeringen C och beräknas R enligt formeln (du kan välja och R, men det rekommenderas att välja C, av noggrannhetsskäl)

;

Vinsten beräknas Till på U 1 kaskad av 1:a ordningen, som bestäms från förhållandet

,

var Till på Uär förstärkningen av filtret som helhet; Till på U 2 , …, Till på Fn– kaskadförstärkningar av andra ordningen;

Att implementera förstärkning Till på U 1 det är nödvändigt att ställa in motstånden baserat på följande förhållande

R B = R A ּ (Till på U1 –1) .

För att beräkna kaskaden av andra ordningen:

Genom att minska det ockuperade området väljs valörerna av kapacitet C 1 = C 2 = C;

Koefficienterna väljs enligt tabellerna b 1 i och F pi för kaskader av 2:a ordningen;

Enligt det givna värdet på kondensatorer C motstånd beräknas R enligt formeln

;

För den valda filtertypen måste du ställa in lämplig förstärkning Till på Ui = 3 – (1/F pi) av varje steg av den andra ordningen, genom att ställa in motstånden, baserat på följande förhållande

R B = R A ּ (Till på Ui –1) ;

För Bessel-filter, multiplicera värdena för alla kapacitanser med den erforderliga gruppfördröjningen.

Butterworth filter

Butterworth lågpassfilteröverföringsfunktion n-th order karakteriseras av uttrycket:

Frekvenssvaret för ett Butterworth-filter har följande egenskaper:

1) I valfri ordning n frekvenssvarsvärde

2) vid gränsfrekvensen u=u s

Lågpassfiltrets frekvensgång minskar monotont med ökande frekvens. Av denna anledning kallas Butterworth-filter filter med de mest platta egenskaperna. Figur 3 visar graferna för amplitud-frekvenskarakteristika för Butterworth lågpassfiltret på 1-5 ordningar. Uppenbarligen, ju högre ordningen filtret har, desto mer exakt approximeras frekvenssvaret för ett idealiskt lågpassfilter.

Figur 3 - Frekvenssvar för ett Butterworth lågpassfilter i storleksordningen 1 till 5

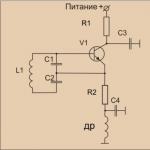
Figur 4 visar en schematisk implementering av Butterworth HPF.

Figur 4 - HPF-II Butterworth

Fördelen med Butterworth-filtret är det jämnaste frekvenssvaret vid passbandsfrekvenser och dess minskning till nästan noll vid undertryckningsbandsfrekvenser. Butterworth-filtret är det enda som bevarar formen på frekvenssvaret för högre ordrar (med undantag för den brantare rolloffen vid cutoff), medan många andra typer av filter (Bessel-filter, Chebyshev-filter, elliptiskt filter) har olika form av frekvenssvaret i olika ordningsföljder.

Jämfört med Chebyshev Type I- och II-filter eller ett elliptiskt filter har Butterworth-filtret en plattare rolloff och måste därför vara av högre ordning (vilket är svårare att implementera) för att ge önskad prestanda vid gränsfrekvenserna.

Chebyshev filter

Kvadraten på modulen för överföringsfunktionen för Chebyshev-filtret ges av:

var är Chebyshev-polynomet. Modulen för överföringsfunktionen för Chebyshev-filtret är lika med en vid de frekvenser där den försvinner.

Chebyshev-filter används vanligtvis där det krävs att ge de erforderliga frekvenssvarsegenskaperna med ett lågordningsfilter, i synnerhet bra frekvensundertryckning från undertryckningsbandet, medan jämnheten i frekvenssvaret vid passband och undertryckningsfrekvenser inte är så viktigt .

Det finns Chebyshev filter I och II släkten.

Chebyshev filter av den första sorten. Detta är en vanligare modifiering av Chebyshev-filter. I passbandet för ett sådant filter är krusningar synliga, vars amplitud bestäms av krusningsindexet e. I fallet med ett analogt elektroniskt Chebyshev-filter är dess ordning lika med antalet reaktiva komponenter som används i dess implementering. En brantare avklingning av karakteristiken kan erhållas om rippel tillåts inte bara i passbandet, utan även i undertryckningsbandet, genom att addera nollor till filtrets överföringsfunktion på den imaginära axeln jsh i det komplexa planet. Detta kommer emellertid att resultera i mindre effektiv undertryckning i undertryckningsbandet. Det resulterande filtret är ett elliptiskt filter, även känt som ett Cauer-filter.

Frekvenssvaret för Chebyshev-lågpassfiltret av fjärde ordningen av det första slaget visas i figur 5.

Figur 5 - Frekvenssvar för Chebyshev lågpassfilter av den första typen av fjärde ordningen

Typ II Chebyshev-filtret (inverterat Chebyshev-filter) används mer sällan än Type I Chebyshev-filtret på grund av den mindre branta rolloffen av amplitudsvaret, vilket leder till en ökning av antalet komponenter. Den har ingen rippel i passbandet, men finns i undertryckningsbandet.

Frekvenssvaret för Chebyshev-lågpassfiltret av den andra typen av fjärde ordningen visas i figur 6.

Figur 6 - Frekvenssvar för Chebyshev lågpassfilter av den andra typen

Figur 7 visar kretsimplementationer av Chebyshev HPF av I- och II-ordningarna.

Figur 7 - Chebyshev HPF: a) Jag beställer; b) II ordning

Egenskaper för frekvensegenskaperna hos Chebyshev-filter:

1) I passbandet har frekvenssvaret en likavågskaraktär. På intervallet (-1? u? 1) finns n punkter där funktionen når ett maximalt värde på 1 eller ett minimivärde på . Om n är udda, om n är jämnt;

2) värdet på frekvenssvaret för Chebyshev-filtret vid gränsfrekvensen är

3) För minskar funktionen monotont och tenderar till noll.

4) Parametern e bestämmer ojämnheten i frekvenssvaret för Chebyshev-filtret i passbandet:

Jämförelse av frekvenssvaret för Butterworth- och Chebyshev-filtren visar att Chebyshev-filtret ger mer dämpning i passbandet än Butterworth-filtret av samma ordning. Nackdelen med Chebyshev-filter är att deras fas-frekvensegenskaper i passbandet skiljer sig avsevärt från linjära.

För Butterworth- och Chebyshev-filter finns det detaljerade tabeller som visar koordinaterna för polerna och koefficienterna för överföringsfunktionerna för olika beställningar.

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> LPF1)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> HPF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> PF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> RF)

Butterworth filtrerar 4 beställningar

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> LPF1)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> HPF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> PF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> RF)

Chebyshev filter 3 beställningar

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> LPF1)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> HPF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> PF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> RF)

Chebyshev filter 4 beställningar

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> LPF1)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> HPF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> PF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> RF)

3:e ordningens Bessel-filter

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> LPF1)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> HPF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> PF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> RF)

4 order Bessel filter

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> LPF1)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> HPF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> PF)

KONVERTERING AV FREKVENSEGENSKAPER FÖR DF (LPF --> RF)

Analysera effekten av fel vid inställning av koefficienterna för det digitala lågpassfiltret på frekvenssvaret (genom att ändra en av koefficienterna b j). Beskriv arten av förändringen i frekvenssvar. Gör en slutsats om effekten av att ändra en av koefficienterna på filtrets beteende.

Vi kommer att analysera inverkan av fel vid inställning av de digitala lågpassfilterkoefficienterna på frekvensgången med hjälp av exemplet med ett 4:e ordningens Bessel-filter.

Vi väljer värdet på avvikelsen för koefficienterna ε lika med –1,5 %, så att den maximala avvikelsen för frekvenssvaret är cirka 10 %.

Frekvenssvaret för det "ideala" filtret och filter med modifierade koefficienter med värdet på ε visas i figuren:

Och

Av figuren kan man se att förändringen i koefficienterna b 1 och b 2 har störst inverkan på frekvensgången (deras värde överstiger värdet av andra koefficienter). Med ett negativt värde på ε noterar vi att positiva koefficienter minskar amplituden i den nedre delen av spektrumet, medan negativa koefficienter ökar den. Med ett positivt värde på ε händer allt tvärtom.

Kvantisera det digitala filtrets koefficienter med ett sådant antal binära siffror att den maximala avvikelsen för frekvenssvaret från det ursprungliga är cirka 10 - 20 %. Skissa frekvensgången och beskriv karaktären av dess förändring.

Genom att ändra antalet siffror i bråkdelen av koefficienterna b j Observera att den maximala avvikelsen för frekvenssvaret från originalet, som inte överstiger 20 %, erhålls vid n≥3.

Typ av frekvensgång för olika n visas i figurerna:

n \u003d 3, maximal avvikelse av frekvenssvar \u003d 19,7 %

n \u003d 4, maximal avvikelse av frekvenssvar \u003d 13,2 %

n \u003d 5, maximal avvikelse för frekvenssvaret \u003d 5,8 %

n \u003d 6, maximal avvikelse av frekvenssvar \u003d 1,7 %

Det kan således noteras att en ökning av bitdjupet under kvantisering av filterkoefficienterna leder till det faktum att filtrets frekvenssvar mer och mer tenderar mot den ursprungliga. Det bör dock noteras att detta komplicerar den fysiska implementeringen av filtret.

Kvantisering för olika n kan ses på bilden: